This chapter illustrates the construction of some basic exploratory data analysis graphs. More complex graphs are considered in Chapter 15, although at times we will see graphs presented in conjunction with particular statistical analysis techniques in other chapters. In this chapter, we concentrate on data taking continuous values initially, but a short section on graphs for discrete valued variables is also included.
There are many ways to create statistical graphs. The traditional method uses one of the base R packages, but in recent years, the ggplot2 package has gained considerable attention. The presentation of both styles of graph are given throughout this chapter. You will need to ensure the ggplot2 package is available for use in your R session by issuing the command:
It is common for R users to access the variables after issuing the command
The detach() command undoes the attach() command. To remove the “attachment", you will issue the command detach(airquality).
You could look at the help file for this data if you wanted to learn its complete story using ?airquality. It tells us that the data are for daily readings of the following air quality values for May 1, 1973 (a Tuesday) to September 30, 1973 (a Sunday).
This data suits our purposes for the majority of examples in this chapter but we will also need to look at another data set for the discussion of graphs for discrete valued variables.
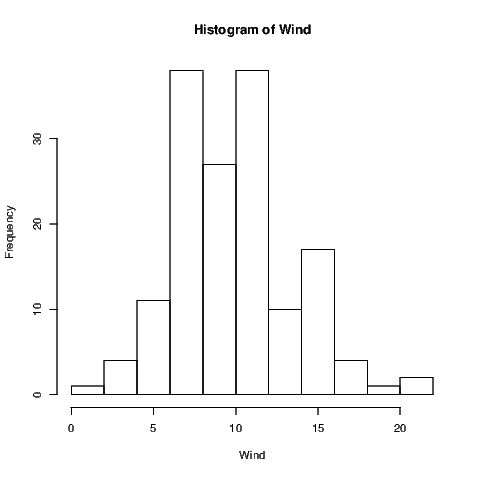
Like many graphical functions in R, the hist() command will attempt to make a suitably attractive histogram with the minimum of input from the user. Exhibit 7.1 shows what results from the simplest application of the hist() command.
Note that the figure created has default settings for the main title, axis labels and that the number of classes (also called bins) and the cutoffs between them have been chosen automatically. Various methods exist for these choices, but it is my recommendation that the user find out what happens when the default settings are chosen and then alter only what is actually necessary. For example, graphs in this document do not always need the default title inserted so we need to suppress the default action if we want to remove the title. We may also want more informative axis labels. Both of these alterations are done for the creation of Exhibit 7.2.

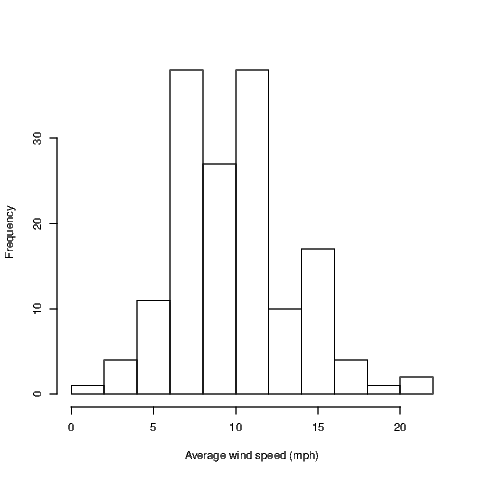
Variable names should be informative but aren’t always what we want to see in graphs. Notice that in Exhibit 7.2, I’ve made the x-axis label more informative by indicating the units of measurement for the wind speed. As I already have a caption for my Exhibit, I have chosen to remove the default title by adding the argument main="" to the hist() command.
Aside from the alteration of the default axis label and the change in the main title for our histograms, we could make quite a number of changes. The hist() function allows the user various options for the way the bars are filled in for example. It’s often worth checking the default behaviour and then seeing if the resulting graph is what you want. If it isn’t, then investigate your options by looking at the relevant help file; in this case type ?hist to get to the help for the hist() function.
Other graphs we create will show points marked with small hollow circles; we may wish to make these circles smaller, joined by line segments, filled in, a different colour or combinations of these attributes. The par() function should be investigated to find out what is possible. Most graph functions allow the user the option of adding arguments that will be passed directly to the par() function to obtain the same behaviour. Investigate the graphical parameters at some stage using ?par but be warned, there are lots of adjustments that can be made. Experimenting is really the only option when it comes time to get your graph looking perfect.
Additional text and/or lines can be added to some graph types. It may prove useful to show the line of best fit along with the data (illustrated in Chapter 12) for example. We’ll see how to do the fancy things in Chapter 15.
Histograms aren’t the “be all and end all" for univariate summary graphs. As a case in point, they aren’t at all useful for small sample sizes. Various other graphs appear in introductory statistics courses and that is why they appear here. I don’t mean to support one over another at all — that’s up to you to determine.
Boxplots show us quickly the shape of the distribution of a sample. They show the median, lower and upper quartiles, and the minimum and maximum of a sample. They will also identify points as outliers if these points are too far from the bulk of values in the sample.
Exhibit 7.3 shows us the boxplot for the average wind speed at LaGuardia airport. Notice that I have added an additional command to set up the size of the graph window. The windows() command has various aliases — x11(), X11(), win.graph() — none of which are required if the standard width and height of the graph window are acceptable. You may wish to see why I’ve changed the height of the graph window by ignoring the windows() command from Exhibit 7.3
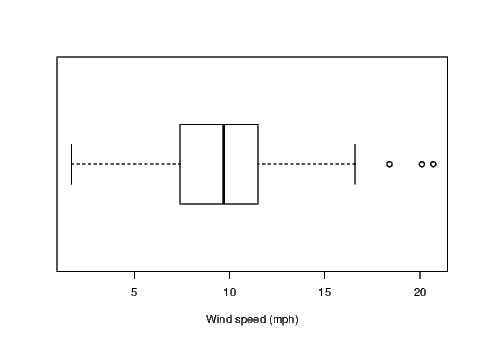
Notice that I’ve changed the default orientation of the boxplot by adding the argument horizontal=TRUE to the boxplot() command. I have also ensured the more informative axis label for wind speed is included using the xlab argument in the command.
Boxplots are often useful for comparing several small samples at once. We must ensure that the same axis is used for the units of measure of interest and the easiest way to ensure this is to put the various samples into the same graphic with only one axis rather than having a series of single boxplots each having their own axis.
For the purposes of illustration, I want to show the distribution of the daily average wind speeds for the five months separately.
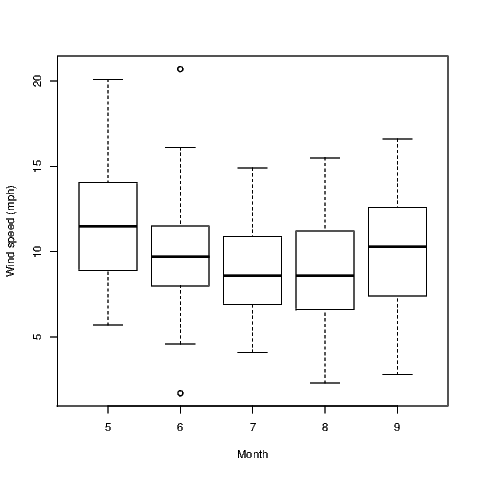
The comparative boxplot is created using a formula to describe the relationship between the two variables that are referred to in our graph. The use of the tilde symbol between Wind and Month could be read as something like “average wind speed depends on the month" — well a theory that might be illustrated in our graph anyway. Certainly it is the potential for this relationship to exist that may be exposed through use of the comparative boxplot.
Dotplots aren’t everyone’s cup of tea but they are frequently offered as substitutes for boxplots and histograms. Again, I chose to alter the default window size for the example given in Exhibit 7.5 because I didn’t like the way the regular graph window presented this graph.

Some people find the standard dotplot that R creates a little artificial. The spacing between points horizontally and vertically is captured by the human eye, but this graph is a single dimensional representation. Adding jitter to the data allows points where there are ties to be represented by a pair of points on the graph rather than two perfectly overlaid points which look like a single point. The jitter() command can be embedded within the command for creation of a dotplot, but is not required for our example data as there are no ties. If there were a large number of ties, we would have used the command dotchart(jitter(Wind)).
Occasionally it’s useful to see how a measurement changes over the time the data were collected. R does this very simply using the plot() command as shown in Exhibit 7.6 which is for the maximum daily air temperatures at LaGuardia airport from 1 May to 30 September 1973. We can see periods of time where the maximum temperatures were fairly consistent and periods where it was fairly volatile. The middle of the graph is for the month of July which is the height of summer in New York and as a consequence we expect to see few points nearer the lower part of the graph during this period.
Notice that we have altered the range of values covered by the y-axis using a specific command. The ylim has a corresponding xlim to create limits for the x-axis. Adding one more argument to the plot() command will change the plotting from points to lines (shown in Exhibit 7.7). Combinations of points and lines can be obtained (not shown); the user can also alter the style of the points and lines being printed.
There is a simpler way to generate time series plots which we demonstrate in Chapter 14. It is easier to augment this line plot than the time series plot, and in so doing we will gain an insight into how other plots like the time series plot are created.
The most common quantile-quantile plot we might wish to create is used to investigate the usefulness of the normal distribution to model a variable’s distribution. Normal quantiles are created automatically for the normal quantile plot when it is generated using the qqnorm() command. The default plot for this is shown in Exhibit 7.8.
If these data were normally distributed, the points on the plot would lie on a straight line. The qqline() command adds the straight line to the plot to assist with determining the linearity of the points.
Scatter plots are created using the plot() command by one of two methods. Exhibit 7.9 was created using
but the same plot can be generated using what is known as a formula. In this case, only one argument is given to the plot() command but both variables of interest are in that argument.
The tilde symbol is often read as “…is distributed as…" but we might simplify this to be read as “follows". This makes some sense as we generally create a scatter plot to see if one variable follows the other; in this case we are seeing if temperature depends on wind speed in some way.
A scatter plot matrix is just a matrix of scatter plots where each variable is plotted against all other variables. This graphic is therefore very useful for a preliminary look at multivariate data. In R, we obtain this graphic using the pairs() command as illustrated in Exhibit 7.10.
Only four of the variables within the air quality data have been used in this example because the variables for the month and day take discrete values and therefore do not suit scatter plots — take a look for yourself if you must but it’s probably better to think about why this is the case before you look at the graphs. To select the four variables of interest, I have created a data.frame with the variables I want included; this data.frame() command is then nested within the pairs() command.
Note that the names of the variables appear in the spaces on the leading diagonal and that the graphs on either side of the diagonal plot the same data but with the axes reversed. Sometimes the human eye will pick up a relationship when the data are presented one way better than the other way.
R does not contain many graphs for discrete valued variables.
If a variable is considered by R to be a factor, then the default action of the plot() command is to construct a bar chart. This is illustrated using a data set which is part of the default installation of R called state.region examined using
Given this variable is a factor with four levels it is well suited to presentation in a bar chart, as seen in Exhibit 7.11.
This figure was created from the raw data, that is the regions for each of the fifty states in the U.S. If we had summary data with counts for each of the categories, we would need to use the barplot() command. The summary() command shows us how many states fall into each category in this instance.
These values are then plotted in Exhibit 7.12.
While this data set is rather trivial, it is useful for demonstrating one more feature. Note that both in the output above and in Exhibit 7.11, the Western region is the last category. To reorder the regions in the bar chart is actually fairly straight forward. All we need to do is make a small addition to the existing commands.
and re-create the bar chart accordingly (see Exhibit 7.13).
OK, if you must do so, make a pie chart using the pie() command. Even the help for this command says they are a bad representation for data, stating “Pie charts are a very bad way of displaying information. The eye is good at judging linear measures and bad at judging relative areas. A bar chart or dot chart is a preferable way of displaying this type of data."
The pie chart for the state.region data is given in Exhibit 7.14.
If you are carrying on working with R you might wish to remove direct access to the data sets we used in this chapter by issuing the following commands