Maindonald, John

Use of the Beta-binomial for Modeling Dose-Mortality Data

Statistics Research Associates, Wellington

In the exposure-mortality data that is of interest, the exposure measure may be time in coolstorage, or exposure to varying levels of a fumigant for a fixed time period. Each replicate provides information, for each of a number of exposure levels, on mortality. There are then several replicates for each combination of one or more species and/or lifestage and/or temperature or other conditions. The aim is to compare tolerance between species/lifestage combinations, and to predict, if possible, a level of exposure that is likely to lead to close to 100% mortality.

Abilities have recently been added to the glmmTMB package for R that facilitate the use of models that assume a beta-binomial error, with the scale parameter modeled as a function of explanatory variables. Lines (or, in principle, curves), fitted assuming a suitable link function, can be modeled either as fixed or as random effects. Possibilities are a random intercept that is drawn from a normal distribution, or a random bivariate normal intercept and slope.

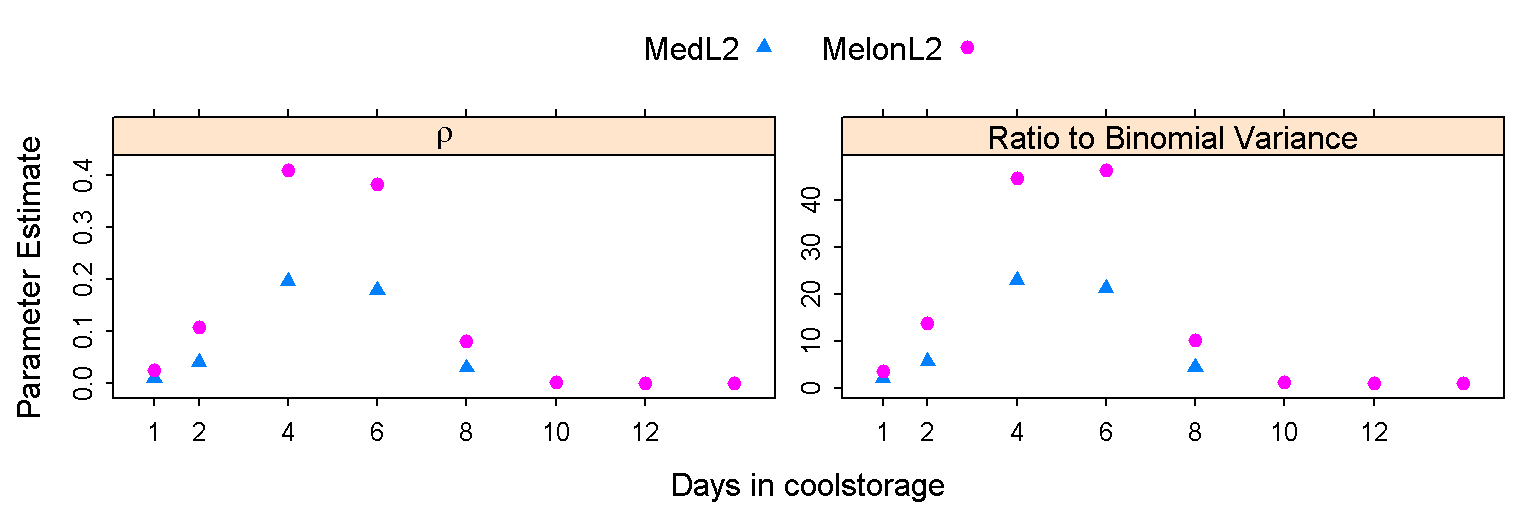
Interesting and important implications, not previously considered in the analysis of organic produce quarantine data, or in the design of the relevant experiments, flow from the modeling of the scale parameter. It is easiest to explain how these effects operate when expressed in terms of the intra-class correlation \(\rho\), which is a simple function of glmmTMB’s choice of scale parameter. The graph shows the estimated patterns of change of \(\rho\) with days in coolstorage, for the larval 2 lifestages of two different fruitfly species, in one dataset examined. Predicted mortalities range from 1 day:0.08; 4: 0.44; 8:0.999 for MedL2, and 1:0.14; 4:0.3; 8:0.66 14:0.997 for MelonL2.

An intra-class correlation of \(\rho\) implies that, given a probability \(\pi\), the variance cannot be reduced below \(\pi(1-\pi)\rho\), no matter how large the sample size \(n\). Thus, if \(\rho = 0.1\), the variance cannot be reduced below \(0.1 \pi(1-\pi)\). A sample size of 90 reduces it to 10% above this minimum. Points to note are:

• The assumption that the binomial variance is multiplied by an amount that is the same at all points on the scale, as commonly made when analyzing using quasibinomial errors, gives much too much weight to points at mid-range mortalities, and too little to points at high mortalities.
• A further consequence is that slope estimates will be overly influenced by statistical variation in mid-range mortalities. There are strong implications for the use of insect material.

The beta-binomial may be too extreme in downplaying the benefits of increasing sample size. This calls for further investigation.