Lecture 29 Multicollinearity
29.1 Idea of Collinearity and Orthogonality
Consider the model \[Y = \beta_0 + \beta_1 X_1 + \beta_2X_2 + \varepsilon\] .
We normally interpret the regression parameter \(\beta_1\) as the rate of change in Y per unit change in \(X_1\), where \(X_2\) is kept constant.
However, if \(X_1\) and \(X_2\) are strongly related, then this interpretation may not be valid (or even possible). In particular if \(X_1\) increases, \(X_2\) may increase at the same time. An example would be if \(X_1\)= personal income and \(X_2\) =household income. The effect of \(X_1\) is expressed both directly (through \(\beta_1\)) and indirectly (through \(\beta_2\)). This complicates both the interpretation and the estimation of these parameters.
Now if \(X_1\) and \(X_2\) have a total lack of any linear relationship (uncorrelated) then they are said to be orthogonal.
In practice regressors are rarely orthogonal unless the regression arises from a carefully designed experiment.
Nevertheless a little non-orthogonality is usually not important to the analysis, especially in view of all the other variability involved.
29.2 Non-Orthogonality
However sometimes \(X_1\) and \(X_2\) are so closely related that the regression results are very hard to interpret. For example inclusion of one variable into a model already containing the other variable can radically alter the regression parameters. The parameters may also be very sensitive to slight changes in the data and have large standard errors.
Severe non-orthogonality is referred to as collinear data or multicollinearity. This
- can be difficult to detect
- is not strictly a modeling error but a problem of inadequate data
- requires caution in interpreting results.
So we address the following questions:
- How does multicollinearity affect inference and forecasting?
- How does one detect multicollinearity?
- How does one improve the analysis if multicollinearity is present?
29.3 A Numerical Example
We will consider the effects of multicollinearity in the A and B data considered earlier. Recall the model is
\[Y = 50 + 5\times A + 5\times B + \varepsilon ~~~~ (*) \]
Though you would not have noticed it, the A and B data were highly correlated.
29.5
This is what resulted in the relatively high standard errors for each regression coefficient (given the super high \(R^2\))
Call:
lm(formula = Y ~ A + B, data = sim_final)
Residuals:
Min 1Q Median 3Q Max
-1.36984 -0.74294 -0.05982 0.69150 1.63488
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 48.7641 2.1367 22.82 3.43e-14 ***
A 4.7613 0.3383 14.07 8.48e-11 ***
B 5.2896 0.3500 15.11 2.75e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8985 on 17 degrees of freedom
Multiple R-squared: 0.9977, Adjusted R-squared: 0.9974
F-statistic: 3701 on 2 and 17 DF, p-value: < 2.2e-1629.6
Now suppose we keep exactly the same numbers A, B and epsilon, but break the correlation between the A and B columns.
As a simple way of spreading them out, we just randomize the order of numbers in column B, then recompute Y.
29.8
Call:
lm(formula = Y_rand ~ A + B_rand, data = sim_rand)
Residuals:
Min 1Q Median 3Q Max
-1.37733 -0.75680 -0.02675 0.70378 1.54084
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 50.0187 2.6339 18.99 6.96e-13 ***
A 5.0416 0.1199 42.05 < 2e-16 ***
B_rand 4.9418 0.1240 39.84 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9105 on 17 degrees of freedom
Multiple R-squared: 0.9964, Adjusted R-squared: 0.996
F-statistic: 2372 on 2 and 17 DF, p-value: < 2.2e-16The standard errors of the coefficients are about 1/3 what they were.
Note that really the only thing we have done here is to break the correlation between \(A\) and \(B\), but this has greatly improved the analysis.
29.9 Orthogonal Data
Consider the model \[Y = \beta_0 + \beta_1 X + \beta_2 Z + \varepsilon\]
Recall that if \(X\) and \(Z\) are uncorrelated, they are called orthogonal. Then
the least squares estimates \(\hat\beta_1\) and \(\hat\beta_2\) are independent of each other
the order of adding the variables does not affect the sums of squares in the ANOVA table.
In other words it doesn’t matter whether we talk about the effect of \(X\) by itself or “\(X\) after \(Z\)”. The effect is the same.
Interpretation of parameters a lot easier.
But it usually only happens in designed experiments with balanced numbers.
In summary, orthogonality of the explanatory variables allows easier interpretation of the results of an experiment and is an important goal in the design of experiments.
29.10 Collinear data
Suppose we have three sets of numbers \(X,Z,Y\) such that \[Y = \beta_0 +\beta_1 X + \beta_2 Z +\varepsilon\]
but that, unknown to us, \[Z = \alpha_0 + \alpha_1 X\] at least equal up to some level of rounding error.
Then the regression model could be rewritten in terms of any arbitrary combination of the X and Z figures, as we can always add on \(k\) lots of \(\alpha_0 + \alpha_1 X\) and then take off \(k\) lots of \(Z\) (as they’re the same thing):
\[\begin{aligned}Y &= \beta_0 +\beta_1 X + \beta_2 Z + k(\alpha_0 + \alpha_1 X) - k Z +\varepsilon\\ & = (\beta_0 + k\alpha_0) + (\beta_1 + k\alpha_1)X + (\beta_2 - k)Z + \varepsilon\end{aligned}\]
for any real number \(k\).
There are an infinite number of possible solutions, and if we do get a numerical answer for the regression coefficients, the particular answer may even just depend on rounding, with different amounts of rounding could give very different answers.
29.11
We describe this situation by saying the regression model is not estimable.
A consequence of such high correlation between the predictor variables is that the regression coefficients may become totally uninterpretable (for example something you know has a positive relationship with the response ends up with a negative coefficient) and the regression coefficients may have very high standard errors.
This is the problem of Multicollinearity.
How do we assess whether it is a real problem in our data?
29.12 Correlations Among The Predictors
We could look at the correlations between the explanatory variables. Since correlation is a measure of linear relationship, then if two variables are highly correlated then it doesn’t make sense to keep them both in the model.
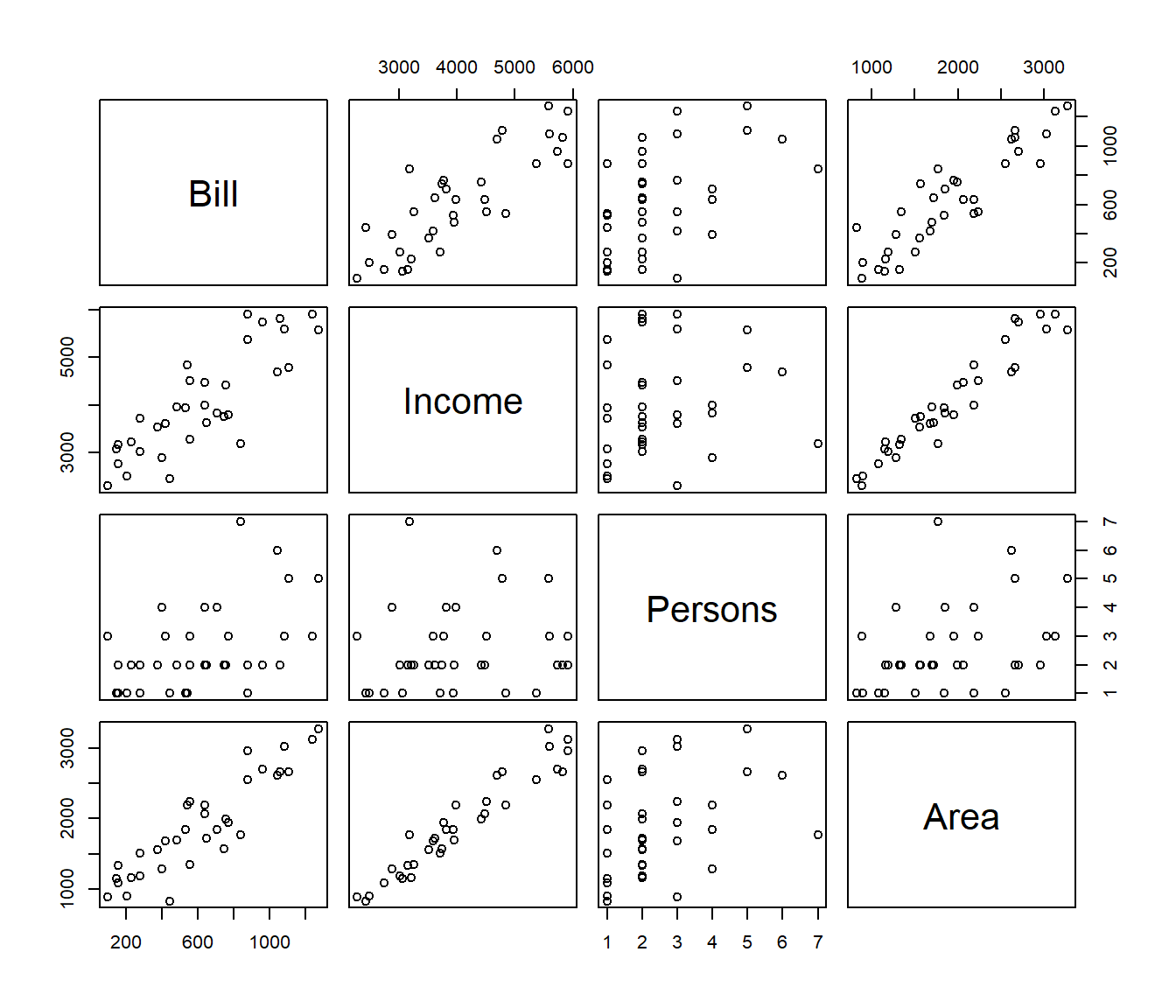
Example. Consider the data below on household electricity bills with explanatory variables
- the income of the household;
- the number of persons in the house; and
- the area of the house.
Each of these explanatory variables would be expected to be related to the Bill, and yet they are also related to each other, so we may not be able to have them all in the same model.
# A tibble: 34 × 4
Bill Income Persons Area
<dbl> <dbl> <dbl> <dbl>
1 228 3220 2 1160
2 156 2750 1 1080
3 648 3620 2 1720
4 528 3940 1 1840
5 552 4510 3 2240
6 636 3990 4 2190
7 444 2430 1 830
8 144 3070 1 1150
9 744 3750 2 1570
10 1104 4790 5 2660
# ℹ 24 more rows29.13
We could check all pair-wise correlations with the cor() function:
Bill Income Persons Area
Bill 1.0000000 0.8368788 0.4941247 0.9050448
Income 0.8368788 1.0000000 0.1426486 0.9612801
Persons 0.4941247 0.1426486 1.0000000 0.3656021
Area 0.9050448 0.9612801 0.3656021 1.0000000This indicates that the Area of the house is very strongly correlated to the Income of the occupants (\(r= 0.961\)), and so both may say much the same thing about the electricity bill. We may not be able to have both these in the model.
By contrast the number of persons in the house is almost unrelated (r = 0.143) to the Income and only weakly related to the Area (r = 0.366) so persons provides more-or-less independent information.
A pairs plot can be useful in these circumstances.
29.15 Spotting multicollinearity
Call:
lm(formula = Bill ~ Area + Persons + Income, data = electric)
Residuals:
Min 1Q Median 3Q Max
-223.36 -102.88 -8.53 78.61 331.46
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -358.44157 198.73583 -1.804 0.0813 .
Area 0.28110 0.22611 1.243 0.2234
Persons 55.08763 29.04515 1.897 0.0675 .
Income 0.07514 0.13609 0.552 0.5850
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 135.4 on 30 degrees of freedom
Multiple R-squared: 0.8514, Adjusted R-squared: 0.8365
F-statistic: 57.28 on 3 and 30 DF, p-value: 1.585e-12The regression as a whole is highly significant, yet none of the regression coefficents are significant. This suggests multicollinearity.
29.16 Contradictory Regression Coefficients
Let’s look at the variable we know are highly correlated (i.e. Area and Income) separately as predictors:
elec.lm1 = lm(Bill ~ Area, data = electric)
elec.lm2 = lm(Bill ~ Income, data = electric)
summary(elec.lm1)
Call:
lm(formula = Bill ~ Area, data = electric)
Residuals:
Min 1Q Median 3Q Max
-216.58 -102.40 -30.67 106.13 292.44
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -211.64863 73.36173 -2.885 0.00695 **
Area 0.43760 0.03635 12.037 2.02e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 144.7 on 32 degrees of freedom
Multiple R-squared: 0.8191, Adjusted R-squared: 0.8135
F-statistic: 144.9 on 1 and 32 DF, p-value: 2.02e-1329.17
Call:
lm(formula = Bill ~ Income, data = electric)
Residuals:
Min 1Q Median 3Q Max
-288.36 -117.01 -46.72 134.27 441.57
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -425.16251 124.92953 -3.403 0.00181 **
Income 0.25899 0.02995 8.649 6.97e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 186.2 on 32 degrees of freedom
Multiple R-squared: 0.7004, Adjusted R-squared: 0.691
F-statistic: 74.8 on 1 and 32 DF, p-value: 6.974e-10By themselves both variables are positively related to Bill and have small Std Errors, as we would expect given the pairs chart.
But let’s see what happens if we put them together:
29.18
Call:
lm(formula = Bill ~ Area + Income, data = electric)
Residuals:
Min 1Q Median 3Q Max
-221.3 -112.4 -19.8 86.4 297.1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -52.23835 120.64872 -0.433 0.668
Area 0.64033 0.12857 4.981 2.27e-05 ***
Income -0.13498 0.08229 -1.640 0.111
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 141 on 31 degrees of freedom
Multiple R-squared: 0.8336, Adjusted R-squared: 0.8228
F-statistic: 77.62 on 2 and 31 DF, p-value: 8.507e-13When put together, one predictor has changed its sign and the Std Errors are much larger.
This illustrates how multicollinearity can render the regression coefficients quite misleading, as presumably income IS related to higher electricity bills (as folk on higher incomes can afford to have more stuff that consumes energy).
29.19
One solution to multicollinearity is to delete one of the variables. However it can be difficult to decide which one to delete. For example suppose we particularly want to quantify the effect of Persons on the electricity bill after adjusting for one of the others:
elec.lm4 = lm(Bill ~ Area + Persons, data = electric)
elec.lm5 = lm(Bill ~ Income + Persons, data = electric)
summary(elec.lm4)
Call:
lm(formula = Bill ~ Area + Persons, data = electric)
Residuals:
Min 1Q Median 3Q Max
-223.77 -101.97 -13.34 83.17 322.35
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -255.94923 70.14230 -3.649 0.000959 ***
Area 0.40429 0.03615 11.183 2.08e-12 ***
Persons 42.03394 16.67947 2.520 0.017096 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 133.9 on 31 degrees of freedom
Multiple R-squared: 0.8499, Adjusted R-squared: 0.8402
F-statistic: 87.74 on 2 and 31 DF, p-value: 1.72e-1329.20
Call:
lm(formula = Bill ~ Income + Persons, data = electric)
Residuals:
Min 1Q Median 3Q Max
-220.49 -105.87 -22.33 85.43 345.76
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -575.4106 95.9010 -6.000 1.23e-06 ***
Income 0.2421 0.0222 10.905 3.89e-12 ***
Persons 85.3352 16.0031 5.332 8.28e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 136.6 on 31 degrees of freedom
Multiple R-squared: 0.8437, Adjusted R-squared: 0.8336
F-statistic: 83.68 on 2 and 31 DF, p-value: 3.204e-13Should we estimate that each extra person adds 42 to the electric bill, or 83 to the bill? Of course the interpretation of these regression models differs slightly (in the first model it is the effect of each additional person among families of the same income, while in the second it is the effect of person among families of with homes of the same area). But it still makes one uneasy to see such a big difference.
29.21 Regressing The Predictors Among Themselves
More generally (more than just looking at individual correlations) we could look at whether any of the variables are strongly predicted by a combination of the other regressors.
i.e. Whether the \(R^2\) for regressing variable \(X_i\)
on the other regressors
\(X_1, X_2,..., X_{i-1}, X_{i+1},...,X{p}\) is large. We call this \(R^2_i\).
If it is large then we probably don’t need \(X_i\) (or some other variables) in the model.
This is more general than just looking at simple correlations between variables, since the regression model picks up on combinations of variables.
A “rule of thumb” is that multicollinearity is a big problem if \(R_i^2 > 0.9\), i.e. the \(i\)th variable is more than 90% explained by the other predictors.
We can get \(R_i^2\) by doing the regressions ourselves, but it is easier to consider the concept of variance inflation instead.
29.22 Variance Inflation Factors, VIFs
A major impact of multicollinearity is found in the variances (and hence standard errors) of the regression coefficients.
- If \(X_i\) is alone in the model \[Y =\beta_0 +\beta_1 X_i +\varepsilon~,~~~~~\mbox{then}\]
\[\hat{\mbox{var}}(\hat\beta_1) = \frac{s^2}{(n-1)\mbox{var}(X_i)}\] 2. If \(X_i\) is in a model with other predictors then \[\hat{\mbox{var}}(\hat\beta_i) = s^2 \left(X^T X\right)^{-1}_{ii}\] where the last term is the corresponding diagonal entry of the \((X^T X )^{-1}\) matrix, the variance-covariance matrix.
29.23
It turns out that we can rewrite this as:
\[\hat{\mbox{var}}(\hat\beta_i) = \frac{s^2}{(n-1)\mbox{var}(X_i)}\cdot \frac{1}{1 - R_i^2}\] where \(R_i^2\) is the multiple \(R^2\) of the regression of \(X_i\) on the other predictors.
Thus, when going from a model with just \(X_i\) to a full model, the variance of the coefficent of \(X_i\) inflates by a factor of
\[\mbox{VIF}_i = \frac{1}{1 - R_i^2}\]
Variable inflation factors that are large (e.g. \(\mbox{VIF}_i > 10\)) indicates multicollinearity problems.
On the other hand if the VIF is around 1, then the variable \(X_i\) is pretty much orthogonal to the other variables.
29.24
To obtain VIFs we need to invoke library(car).
Area Persons Income
44.141264 3.421738 39.035444 Clearly we need to do something to reduce the multicollinearity.
What we do is application-specific! We might choose to remove a variable, or we might choose to do something else (e.g. find a better measure or somehow combine the variables into some average?)
29.25 Example: SAP Data
The following example illustrates multicollinearity in a context where it is not immediately visible. Chatterjee and Price discuss a dataset relating Sales S to A (advertising expenditure), A1 (last year’s advertising), P (promotion expenditure), P1 (last year’s promotions expenditure) and SE (sales expenses). The analyst eventually found out that an approximate budgetary constraint
\[ A + A1 + P + P1 = 5 \] was hidden in the data. The constraint was known to the advertising executives who had commissioned the study but it had not been mentioned to the statistical consultant who was given the data to analyze.
# A tibble: 22 × 6
A P SE A1 P1 S
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1.99 1 0.3 2.02 0 20.1
2 1.94 0 0.3 1.99 1 15.1
3 2.20 0.8 0.35 1.94 0 18.7
4 2.00 0 0.35 2.20 0.8 16.1
5 1.69 1.3 0.3 2.00 0 21.3
6 1.74 0.3 0.32 1.69 1.3 17.8
7 2.07 1 0.31 1.74 0.3 18.9
8 1.02 1 0.41 2.07 1 21.3
9 2.02 0.9 0.45 1.02 1 20.5
10 1.06 1 0.45 2.02 0.9 20.5
# ℹ 12 more rows29.26
We start with a linear model for sales in terms of all other variables:
Call:
lm(formula = S ~ A + P + SE + A1 + P1, data = SAP)
Residuals:
Min 1Q Median 3Q Max
-1.8601 -0.9847 0.1323 0.7017 2.2046
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -14.194 18.715 -0.758 0.4592
A 5.361 4.028 1.331 0.2019
P 8.372 3.586 2.334 0.0329 *
SE 22.521 2.142 10.512 1.36e-08 ***
A1 3.855 3.578 1.077 0.2973
P1 4.125 3.895 1.059 0.3053
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.32 on 16 degrees of freedom
Multiple R-squared: 0.9169, Adjusted R-squared: 0.8909
F-statistic: 35.3 on 5 and 16 DF, p-value: 4.289e-0829.27
We see that, apart from Sales Expenses, there is only weak evidence of a relationship between advertising, promotions and sales.
A P SE A1 P1
36.941513 33.473514 1.075962 25.915651 43.520965 The VIF shows high multicollinearity for all advertising and promotions data.
29.28
If we drop one of the variables the others change their coefficients unpredictably depending on which variable we drop.
SAP.lm2 = lm(S ~ P + SE + A1 + P1, data = SAP)
SAP.lm3 = lm(S ~ A + P + SE + P1, data = SAP)
SAP.lm2 |>
tidy()# A tibble: 5 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 10.5 2.46 4.28 0.000510
2 P 3.70 0.757 4.89 0.000138
3 SE 22.8 2.18 10.5 0.00000000804
4 A1 -0.769 0.875 -0.880 0.391
5 P1 -0.969 0.742 -1.31 0.209 # A tibble: 5 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 5.76 2.70 2.14 0.0475
2 A 1.15 0.967 1.19 0.252
3 P 4.61 0.830 5.56 0.0000347
4 SE 22.7 2.15 10.6 0.00000000666
5 P1 0.0315 0.862 0.0365 0.971 29.29
Suppose we look at the relationships among the predictor variables:
# A tibble: 5 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 4.61 0.145 31.8 1.35e-16
2 P -0.871 0.0446 -19.5 4.38e-13
3 SE 0.0510 0.128 0.397 6.96e- 1
4 A1 -0.863 0.0515 -16.7 5.33e-12
5 P1 -0.950 0.0437 -21.7 7.65e-14This is approximately A = 5 - P -A1 - P1 as in the hidden constraint.
29.30 What do we do about multicollinearity?
As far as 161.251 is concerned, we have few options.
We can remove one (or more) of the correlated variables from the regression. Our aim is to fix the problem, but sometimes we have a bit of choice which variable to remove, in which case we would like the model to be as interpretable as possible. Sometimes the choice is between a variable with many missing values and one with few, and so we choose the latter if it allows us a bigger effective sample size \(n\).
We could construct another variable which is a combination of the two most highly correlated variables. It might be an ordinary average \((X_1+X_2)/2\), or an average of standardized versions of the \(X_i\)s or some other linear combination. Sometimes subtracting or dividing one variable by another will help. For example the incidence of a particular disease such as obesity may be higher in countries with high GDP and high Population. But GDP depends on the size of the economy, which is correlated with the Population. Dividing gives us per capita GDP which is a better indicator of average wealth and hence may be more related to disease incidence.
29.31
- (Not examinable) Those who have studied multivariate statistics may find it useful to construct principal components or do a factor analysis of a set of correlated variables. Dropping less important components leads to a class of models called biased regression. Another form of biased regression shrinks the regression coefficients towards zero - a method called shrinkage estimators.
- (Not examinable) It is possible to fit regression models that impose linear constraints on the regression coefficients (such as forcing them to add to 100%). Such restricted least squares is also beyond the scope of this course. Therefore for this course we focus on method 1, dropping variables.