Lecture 27 Variable Selection
27.1 From model comparison to model selection
In Lecture 26, the scientific question gave us a reduced model and a full model to compare. We knew in advance which additional terms we wanted to test.
Real modelling problems are usually messier. We may have several plausible predictors and a lot of reasonable-looking models, with no single reduced-versus-full comparison that settles the question.
At that point we have moved from model comparison to model selection.
The central question is:
How do we balance model fit against model complexity when several models are plausible?
27.1.1 What are we trying to do?
Before choosing a model, identify the modelling goal:
- Explanation or inference: estimate and interpret effects after adjustment for other variables.
- Prediction: predict new observations accurately.
- Description: find a compact model that describes the observed relationships.
These are different jobs, and they can favour different models. A variable might matter scientifically without helping prediction much, while a strong predictor does not automatically have a causal interpretation.
27.2 Overfitting and underfitting
So why not just put everything into the model?
Warning in geom_segment(aes(x = 1.4, xend = 8.6, y = 0, yend = 0), arrow = grid::arrow(ends = "both", : All aesthetics have length 1, but the data has 3 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.
Figure 27.1: The bias-variance trade-off as model flexibility changes.
This is the bias-variance trade-off. A model that is too simple can omit structure. A model that is too complicated can fit accidental features of the current data and produce less stable estimates.
27.2.1 What if \(\beta=0\)?
Suppose one candidate variable really has coefficient \(\beta=0\). If we leave it out, the remaining coefficients and predictions are usually estimated more precisely. If we include it anyway, we spend a degree of freedom estimating something that is not contributing signal.
That is one form of overfitting: the model is more complicated than it needs to be.
27.2.2 What if \(\beta \ne 0\)?
The opposite mistake is to leave out a variable that really belongs in the model. That is underfitting.
If the omitted predictor overlaps with predictors that remain in the model, their coefficient estimates can be biased because they are now being asked to absorb some of the missing structure. Predictions can also be biased because the fitted mean structure is wrong.
The awkward part is that we do not know in advance which coefficients are truly zero. A hypothesis test gives us evidence, but it does not solve the model-selection problem by itself.
27.3 A small simulation
To make this concrete, consider an artificial industrial process where Yield depends on the process temperature at stage A, and may also depend on the temperature at stage B.
We consider the model \[ Y=\beta_0 + \beta_1 A+ \beta_2 B +\varepsilon.\]
We will assume the values of \(A\) and \(B\) and \(\varepsilon\) are given in the data below. The errors are random \(\varepsilon \sim \mbox{Normal}(0, 1)\).
We will use two simple scenarios: one where the larger model is unnecessary, and one where the smaller model leaves something important out.
27.3.1 Scenario 1: \(\beta_0=50\), \(\beta_1=10\) and \(\beta_2=0\).
In the first scenario, \(B\) genuinely does nothing: \[Y = 50 + 10 A + \varepsilon\]
Compare the correct model using \(A\) alone with an unnecessarily larger model that also includes \(B\).
dat <- sim |>
mutate(Y = 50 + 10 * A + epsilon)
lm1 = lm(Y ~ A, data = dat)
lm2 = lm(Y ~ A + B, data = dat)
lst(lm1, lm2) |>
map_dfr(tidy, .id = "model")# A tibble: 5 × 6
model term estimate std.error statistic p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl>
1 lm1 (Intercept) 49.3 2.03 24.2 3.43e-15
2 lm1 A 10.0 0.112 89.4 2.71e-25
3 lm2 (Intercept) 48.8 2.14 22.8 3.43e-14
4 lm2 A 9.76 0.338 28.9 7.01e-16
5 lm2 B 0.290 0.350 0.827 4.19e- 1Adding the unnecessary variable doesn’t introduce bias (\(\hat\beta_1 \approx 10\)), but the standard error of \(\hat\beta_1\) is higher in the misspecified model.
27.4 Under and Overfitting con’t
27.4.1 Scenario 2: \(\beta_0=50\), \(\beta_1=5\) and \(\beta_2=5\).
Now both predictors genuinely matter: \[ Y = 50 + 5 A + 5 B + \varepsilon \]
dat <- sim |>
mutate(Y = 50 + 5 * A + 5 * B + epsilon)
lm1 = lm(Y ~ A, data = dat)
lm2 = lm(Y ~ A + B, data = dat)
lst(lm1, lm2) |>
map_dfr(tidy, .id = "model")# A tibble: 5 × 6
model term estimate std.error statistic p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl>
1 lm1 (Intercept) 57.8 7.57 7.63 4.74e- 7
2 lm1 A 9.58 0.418 22.9 8.94e-15
3 lm2 (Intercept) 48.8 2.14 22.8 3.43e-14
4 lm2 A 4.76 0.338 14.1 8.48e-11
5 lm2 B 5.29 0.350 15.1 2.75e-11When we wrongly omit \(B\), the estimated coefficient for \(A\) is pulled away from its true value. Once both predictors are included, the fitted coefficients are close to the values used to generate the data.
27.4.2 What did the simulation show?
Omitting a needed variable can bias the remaining estimates and predictions, especially when the omitted predictor overlaps with variables retained in the model. Including an unnecessary variable can leave the estimates centred correctly while increasing their standard errors.
In practice we do not know which situation we are in. Model selection therefore requires a modelling goal and criteria that reflect the cost of complexity. A hypothesis test can contribute evidence, but it is not a complete decision rule.
27.5 How should we judge extra complexity?
Adding variables will always make RSS smaller, so that alone cannot tell us whether the extra complexity was worth it. We need criteria that put the improvement in fit into context.
27.5.1 Fit measures
The coefficient of determination
\[R^2 = 1 - \frac{\sum(y_i-\hat y_i)^2}{\sum(y_i-\bar y)^2}\]
measures the proportion of sample response variation accounted for by the fitted model. It does not penalise complexity, so \(R^2\) cannot decrease when variables are added.
Adjusted \(R^2\) accounts for residual degrees of freedom:
\[R^2_{\mathrm{Adj}} = 1 - \frac{\sum(y_i-\hat y_i)^2/(n-p)}{\sum(y_i-\bar y)^2/(n-1)}.\]
It can decrease when an added term does not reduce RSS enough to justify its degrees of freedom. A decrease is evidence against that particular added structure, not proof that the variable should never be used.
The residual standard error is the residual scale estimate:
\[S = \sqrt{\frac{RSS}{df_{\mathrm{residual}}}}.\]
It measures remaining unexplained variation on the response scale. It is useful for comparing fitted models to the extent that they have the same response and observations.
27.6 Partial F tests and AIC
Partial F tests are useful when we have a particular nested change in mind. AIC provides another criterion:
\[AIC = n\log(RSS/n) + 2p + \text{constant},\]
where \(p\) is the number of fitted regression parameters. Smaller AIC is preferred when comparing candidate models fitted to the same response and observations.
Unlike the partial F test, AIC can compare models that are not nested. It is still just a criterion, not a machine for finding the one true model, but it gives us a practical way to trade fit against complexity.
Individual coefficient P-values answer a more specific question about one coefficient under one parameterisation. They should not be treated as a complete model-selection rule.
27.7 Cross-validation: a prediction question
Everything above is based on the data used to fit the model. If prediction is the goal, the more useful question is:
How well does the model predict observations it did not use to fit itself?
The basic cross-validation idea is:
Figure 27.2: The basic cross-validation cycle.
Figure 27.3: Five-fold cross-validation in action.
For now, focus on the idea rather than the implementation. We will use cross-validation in Lecture 28 when we start fitting larger models.
27.8 Select terms, not arbitrary coefficients
One more thing before we start selecting models: a model term is not always the same thing as one coefficient. A four-level factor creates three treatment coefficients, but scientifically it is still one predictor.
Similarly, in
y ~ A * xA:x is one interaction term, even though it can correspond to several interaction coefficients. If we retain an interaction, we normally retain the corresponding main effects as well. This is the hierarchy principle.
27.9 Example: Model Selection for Climate Data
We will build a model for mean July temperature across 36 towns in Aotearoa New Zealand. We have location variables such as latitude, longitude, elevation, coastal location and island, together with summer temperature, sunshine and rainfall.
# A tibble: 36 × 10
Place Lat Long MnJanTemp MnJlyTemp Rain Sun Height Sea NorthIsland
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Kaitaia 35.1 173. 19.3 11.7 1418 2113 80 1 1
2 Kerikeri 35.2 174 18.9 10.8 1682 2004 73 1 1
3 Dargavi… 36 174. 18.6 10.7 1248 1956 20 1 1
4 Whangar… 35.7 174. 19.7 11 1600 1925 29 1 1
5 Auckland 36.9 175. 19.4 11 1185 2102 49 1 1
6 Tauranga 37.7 176. 18.5 9.3 1349 2277 4 1 1
7 Hamilton 37.8 175. 17.8 8.3 1201 2006 40 0 1
8 Rotorua 38.2 176. 17.5 7.3 1439 1948 307 0 1
9 Gisborne 38.7 178 18.7 13.6 1058 2204 4 1 1
10 Taupo 38.7 177. 17.3 6.5 1178 2021 376 0 1
# ℹ 26 more rows27.10 Climate Exploratory Data Analysis
climate |>
pivot_longer(-c(Place, MnJlyTemp)) |>
ggplot() + geom_point(mapping = aes(x = value, y = MnJlyTemp)) + facet_wrap(vars(name),
scales = "free_x", ncol = 4)
27.10.1 Higher winter temperature associations
- Lower elevations (height)
- Lower latitudes (further north)
- Higher longitudes (further east - recall how Ao/NZ is oriented on a map - possibly correlation with latitude, will check next!)
- Higher summer temperatures
- North island (could just be latitude?)
- Increased rainfall - up to a point! (subtropical vs rainy westcoast - interaction with Island/latitude??)
- Closeness to the sea
- Increased sunshine hours
Several of these predictors are clearly telling us partly the same story.
27.11 Climate: Latitude/Longitude and North vs South
The map makes the geography easier to see: the North Island towns are generally warmer, while longitude mostly reflects the orientation of the islands. Elevation also appears to matter, although it may be confounded with whether a town is close to the sea (it cannot really be both!).
So we’d expect some collinearity here and figuring out which are the best variables to be used might take a bit of playing!
27.12 Climate: Latitude/Longitude and North vs South
Let’s start with Latitude, then add in Height and Sea:
27.13 Building the Climate Model
27.13.0.1 Model 1: Lat only
Call:
lm(formula = MnJlyTemp ~ Lat, data = climate)
Residuals:
Min 1Q Median 3Q Max
-3.6992 -0.9786 0.1566 1.0588 4.7930
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 34.42127 3.94299 8.730 3.35e-10 ***
Lat -0.66187 0.09613 -6.885 6.25e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.822 on 34 degrees of freedom
Multiple R-squared: 0.5824, Adjusted R-squared: 0.5701
F-statistic: 47.41 on 1 and 34 DF, p-value: 6.25e-0827.13.0.2 Model 2: Lat + Height
Call:
lm(formula = MnJlyTemp ~ Lat + Height, data = climate)
Residuals:
Min 1Q Median 3Q Max
-2.0607 -0.6215 -0.1021 0.5145 3.9898
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 32.8788366 2.4333203 13.512 5.30e-15 ***
Lat -0.6005121 0.0596687 -10.064 1.38e-11 ***
Height -0.0071984 0.0009542 -7.544 1.12e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.121 on 33 degrees of freedom
Multiple R-squared: 0.8467, Adjusted R-squared: 0.8374
F-statistic: 91.14 on 2 and 33 DF, p-value: 3.639e-1427.13.0.3 Model 3: Lat + Height + Sea
Call:
lm(formula = MnJlyTemp ~ Lat + Height + Sea, data = climate)
Residuals:
Min 1Q Median 3Q Max
-1.7969 -0.4792 -0.0299 0.5042 3.7850
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 31.290016 2.290747 13.659 6.71e-15 ***
Lat -0.587826 0.054584 -10.769 3.59e-12 ***
Height -0.005121 0.001147 -4.463 9.38e-05 ***
Sea 1.294326 0.466063 2.777 0.00909 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.022 on 32 degrees of freedom
Multiple R-squared: 0.8765, Adjusted R-squared: 0.8649
F-statistic: 75.69 on 3 and 32 DF, p-value: 1.275e-1427.13.0.4 First three predictors: assessment
The first three additions agree across the measures we have considered: the added-term P-values are small, \(S\) decreases, and adjusted \(R^2\) increases. This is consistent with retaining Lat, Height and Sea for this candidate model path.
The Height coefficient also changes noticeably when Sea is added. This tells us that the interpretation of Height depends on whether Sea is adjusted for. The predictors overlap in the information they carry, so the coefficient in a multiple regression is a conditional association, not an isolated effect of height.
27.14 Model 4: Adding NorthIsland
Call:
lm(formula = MnJlyTemp ~ Lat + Height + Sea + NorthIsland, data = climate)
Residuals:
Min 1Q Median 3Q Max
-1.2667 -0.5054 -0.2098 0.4707 3.4088
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 21.378217 4.637932 4.609 6.56e-05 ***
Lat -0.375517 0.101816 -3.688 0.000862 ***
Height -0.004416 0.001109 -3.981 0.000385 ***
Sea 1.803422 0.483327 3.731 0.000766 ***
NorthIsland 1.559710 0.647795 2.408 0.022193 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9526 on 31 degrees of freedom
Multiple R-squared: 0.8959, Adjusted R-squared: 0.8825
F-statistic: 66.73 on 4 and 31 DF, p-value: 8.723e-15The added-term P-value is small, and the fit measures improve. The large change in the Lat coefficient tells us that the interpretation of latitude depends on whether NorthIsland is included. It does not, by itself, prove that the new variable is correcting bias.
Why do you think adding North vs South island is useful over and above Latitude? Wouldn’t Latitude do everything here??
27.15 Model 5: Adding Rain
Call:
lm(formula = MnJlyTemp ~ Lat + Height + Sea + NorthIsland + Rain,
data = climate)
Residuals:
Min 1Q Median 3Q Max
-1.2829 -0.5042 -0.1944 0.4422 3.4651
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 19.6651523 4.6317227 4.246 0.000194 ***
Lat -0.3437001 0.1009517 -3.405 0.001900 **
Height -0.0049792 0.0011322 -4.398 0.000127 ***
Sea 1.6435808 0.4802716 3.422 0.001814 **
NorthIsland 1.7682036 0.6430084 2.750 0.010003 *
Rain 0.0003583 0.0002170 1.651 0.109182
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9271 on 30 degrees of freedom
Multiple R-squared: 0.9046, Adjusted R-squared: 0.8887
F-statistic: 56.9 on 5 and 30 DF, p-value: 2.11e-14The evidence for Rain is mixed. Its coefficient P-value is approximately 0.10, while \(S\) decreases and adjusted \(R^2\) increases. These are all in-sample measures, so they do not establish that Rain will improve prediction for new towns. If prediction were the primary goal, this would be a natural case for validation or cross-validation.
27.16 Model 6: Adding Longitude
lm6 = lm(MnJlyTemp ~ Lat + Height + Sea + NorthIsland + Rain + Long, data = climate)
lm6 |>
summary()
Call:
lm(formula = MnJlyTemp ~ Lat + Height + Sea + NorthIsland + Rain +
Long, data = climate)
Residuals:
Min 1Q Median 3Q Max
-1.3360 -0.4832 -0.1712 0.4008 3.2814
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.8938252 21.1286658 0.326 0.746557
Lat -0.3272942 0.1053819 -3.106 0.004216 **
Height -0.0050077 0.0011449 -4.374 0.000144 ***
Sea 1.6381187 0.4853578 3.375 0.002113 **
NorthIsland 1.5548897 0.7352242 2.115 0.043156 *
Rain 0.0004002 0.0002295 1.744 0.091750 .
Long 0.0701947 0.1132443 0.620 0.540196
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9368 on 29 degrees of freedom
Multiple R-squared: 0.9059, Adjusted R-squared: 0.8864
F-statistic: 46.51 on 6 and 29 DF, p-value: 1.402e-13The evidence against adding Long is consistent: its P-value is greater than 0.5, adjusted \(R^2\) decreases, and \(S\) increases. This candidate addition does not improve the fitted model by these measures.
27.17 Climate model-building progression
We have followed one sensible path through the candidate models. That does not prove we have found the only correct formula. The table just puts the evidence from each step in one place.
| Model | Added term | Adjusted R2 | RSE | AIC | Added-term evidence |
|---|---|---|---|---|---|
| lm 1 | Lat | 0.570 | 1.822 | 149.312 | < 0.001 |
| lm 2 | Height | 0.837 | 1.121 | 115.229 | < 0.001 |
| lm 3 | Sea | 0.865 | 1.022 | 109.455 | < 0.001 |
| lm 4 | NorthIsland | 0.883 | 0.953 | 105.283 | < 0.001 |
| lm 5 | Rain | 0.889 | 0.927 | 104.153 | 0.10 |
| lm 6 | Long | 0.886 | 0.937 | 105.679 | > 0.5 |
The table is useful because it shows what each extra term buys us. It still does not replace the modelling goal, subject-matter knowledge, or proper validation if prediction is what we care about.
27.18 Final Model Diagnostic Plots
27.18.1 A final model check
Once we have a plausible mean structure, we still need to check whether the fitted model shows obvious problems with the LINE assumptions.
lm(MnJlyTemp ~ Lat + Height + Sea + NorthIsland + Rain, data = climate).
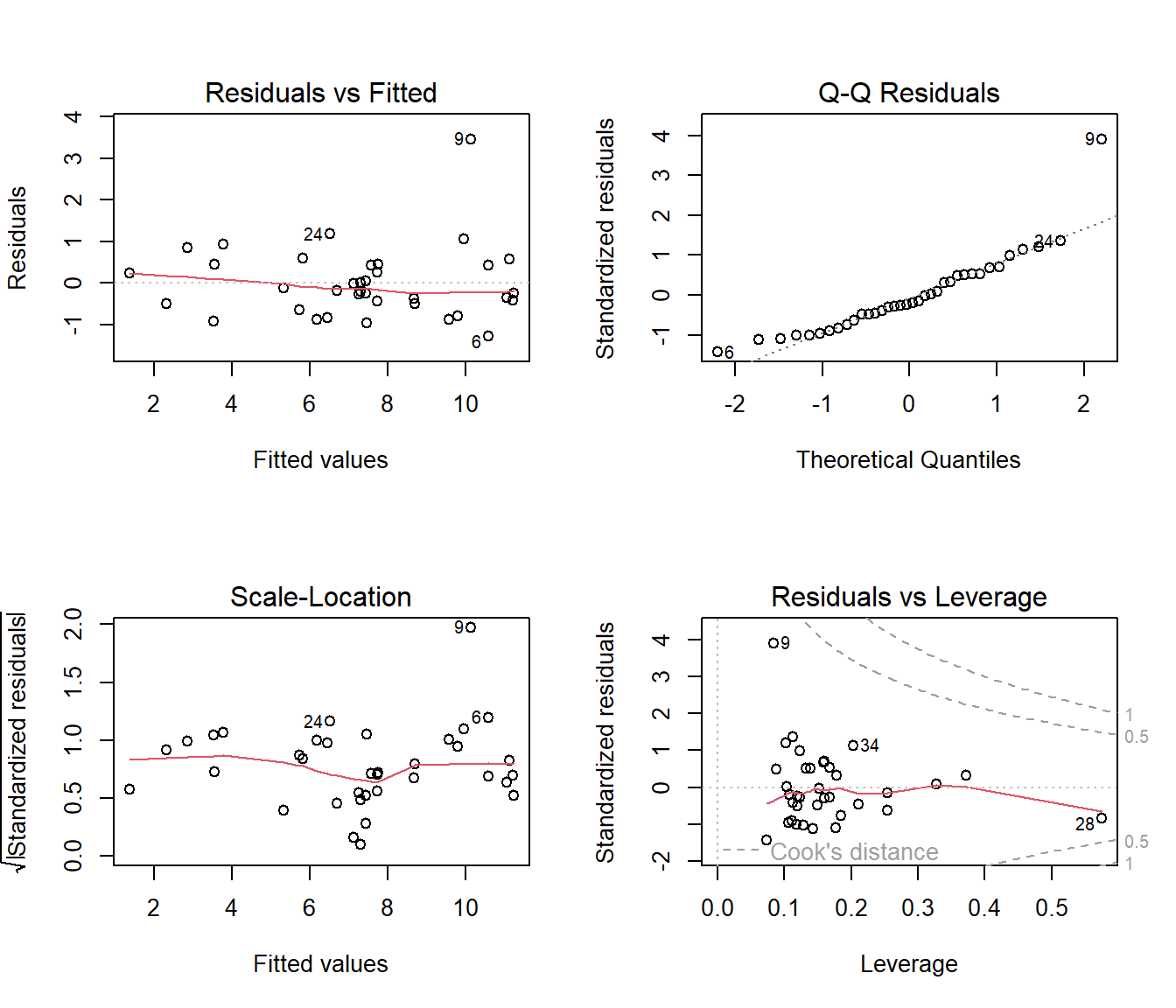
27.18.2 Interpretation of diagnostic plots
- Residuals vs. Fitted: the points show no strong systematic pattern, so there is not strong evidence of a problem with the linear mean structure.
- Normal Q-Q: the points are reasonably close to the reference line, with one noticeable departure. This is not proof of normality, but it gives no strong warning at this scale.
- Scale-Location: the spread does not show a strong trend across fitted values, so there is not strong evidence of changing variance.
- Residuals vs. Leverage: no observation stands out as obviously influential from this plot alone.
These plots do not certify the model. They tell us whether there are obvious departures that need more attention.
27.19 A more realistic running example
From this point in the course, we are going to keep coming back to one more complex dataset rather than starting from scratch with a new toy example each time. The data are hourly bike rentals in Seoul, South Korea, together with weather and calendar variables that might help us explain or predict demand.
We will build this model up as the course goes on. Here we start with several plausible predictors. Later we will come back to the same data for automated variable selection, penalised regression, multicollinearity and the other problems that appear once a model starts looking more like something we would fit in practice.
Download seoul_bike_hourly.csv
# A tibble: 8,760 × 16
date datetime day_index hour rented_bike_count temperature
<date> <dttm> <dbl> <dbl> <dbl> <dbl>
1 2017-12-01 2017-12-01 00:00:00 1 0 254 -5.2
2 2017-12-01 2017-12-01 01:00:00 1 1 204 -5.5
3 2017-12-01 2017-12-01 02:00:00 1 2 173 -6
4 2017-12-01 2017-12-01 03:00:00 1 3 107 -6.2
5 2017-12-01 2017-12-01 04:00:00 1 4 78 -6
6 2017-12-01 2017-12-01 05:00:00 1 5 100 -6.4
7 2017-12-01 2017-12-01 06:00:00 1 6 181 -6.6
8 2017-12-01 2017-12-01 07:00:00 1 7 460 -7.4
9 2017-12-01 2017-12-01 08:00:00 1 8 930 -7.6
10 2017-12-01 2017-12-01 09:00:00 1 9 490 -6.5
# ℹ 8,750 more rows
# ℹ 10 more variables: humidity <dbl>, wind_speed <dbl>, visibility <dbl>,
# dew_point_temperature <dbl>, solar_radiation <dbl>, rainfall <dbl>,
# snowfall <dbl>, season <chr>, holiday <chr>, functioning_day <chr>The response is rented_bike_count. Potential explanatory variables include weather measurements such as temperature, humidity, wind speed and rainfall, as well as calendar information such as hour, season and whether the day is a holiday.
There is no obvious single model here. Several predictors are plausible, some are clearly related to one another, and the number of possible models gets large very quickly. That is exactly why this is useful as a running example.
seoul_basic = lm(rented_bike_count ~ temperature + humidity + wind_speed, data = seoul_hourly)
seoul_richer = lm(rented_bike_count ~ temperature + humidity + wind_speed + visibility +
dew_point_temperature + solar_radiation + rainfall + snowfall + hour + season +
holiday + functioning_day, data = seoul_hourly)
tibble(model = c("basic weather model", "richer weather + calendar model"), adj_r_squared = c(summary(seoul_basic)$adj.r.squared,
summary(seoul_richer)$adj.r.squared), sigma = c(summary(seoul_basic)$sigma, summary(seoul_richer)$sigma),
aic = c(AIC(seoul_basic), AIC(seoul_richer)))# A tibble: 2 × 4
model adj_r_squared sigma aic
<chr> <dbl> <dbl> <dbl>
1 basic weather model 0.376 510. 134080.
2 richer weather + calendar model 0.550 433. 131228.The richer model looks better on all three in-sample criteria: adjusted \(R^2\) is higher, while residual standard error and AIC are lower. That tells us it fits these data better after accounting, to some extent, for the extra complexity. It does not yet tell us that it will predict new bike demand better.
With only a few candidate models we can still do this by hand. Once the predictor list gets longer, that becomes painful. In the next lecture we look at two ways forward: automate the search through candidate models, or keep a larger model and shrink the coefficients instead of repeatedly adding and removing terms.