Lecture 11 Testing in Multiple Regression Models (2)

In class version

In the previous lecture we looked at tests for a relationship between the response and at least one of the predictors in a multiple linear regression model.

In this lecture we will examine another testing method about predictors.

We will begin by looking at tests about a single predictor variable.

11.1 What Precisely Are We Testing?

Consider the following question regarding the NZ Climate example:

Is the mean July temperature related to the number of sunshine hours?

This question is essentially the same as asking, “Does Sun provide useful information about MnJlyTemp”

The answer to this depends on the context in which the question is asked.

For example:

  • Sun may be helpful in understanding MnJlyTemp in the absence of other information;
  • Sun may not provide significant additional information once other explanatory variables are taken into account.

For example, suppose we are modelling a measure of reading ability (response variable) for children at primary school.

We would find that reading ability is related to height.

However, height probably does not provide additional useful information once age is taken into account.

11.2 T Tests for Single Parameters

The summary() command in R (and standard output from other statistical packages) provides information for testing the importance of a covariate “taking into account all other variables in the model”.

When we saw this in the case of simple regression, we were making an adjustment for only the average of responses, not for any other predictors that affect the response.

Specifically, given the model \(Y_i = \beta_0 + \beta_1 x_{i1} + \ldots + \beta_p x_{ip} + \varepsilon_i~~~(i=1,2,\ldots,n)\) the output provides statistics for performing a t test of \[H_0: \beta_j = 0~~\mbox{versus}~~H_1: \beta_j \ne 0\] for any given variable xj, making no assumptions about the other regression parameters.

11.3 T Tests for the Climate Regression Model

Download climate.csv

## Climate <- read.csv(file = "https://r-resources.massey.ac.nz/data/161251/Climate.csv",
##     header = TRUE, row.names = 1)

Consider testing whether MnJlyTemp is related to Sun, and then again having accounted for the other variables Lat and Height.

Climate.lm5 = lm(MnJlyTemp ~ Sun, data = Climate)
Climate.lm5 |>
    tidy() |>
    kable()
term estimate std.error statistic p.value
(Intercept) -1.151124 4.1371927 -0.278238 0.7825148
Sun 0.004295 0.0020775 2.067359 0.0463798

So, if we take a naive look at whether the sunshine hours affect the July temperature, we probably conclude that there is evidence that there is a relationship. This sort of naive investigation is conducted rather too often for my liking.

The correct analysis is to include the variables we know affect the response variable. For example let’s include Lat and Height. (We could include other variables but these are enough to make the point.)

Climate.lm6 = lm(MnJlyTemp ~ Lat + Height + Sun, data = Climate)
Climate.lm6 |>
    tidy() |>
    kable()
term estimate std.error statistic p.value
(Intercept) 34.7991844 3.7668565 9.2382559 0.0000000
Lat -0.6154963 0.0641705 -9.5915784 0.0000000
Height -0.0073314 0.0009824 -7.4628382 0.0000000
Sun -0.0006514 0.0009694 -0.6719237 0.5064548

This test shows that sunchine hours do not provide useful additional information about the July temperature having taken account of (or adjusted for) the other variables.

This does not mean that MnJlyTemp is unrelated to Sun. We saw that it was.

Consider though that this data includes cities and towns. The latitude and altitude of towns and cities is rather unlikely to change. (OK, let’s not debate sea level rises courtesy of climate change just now!)

The number of sunshine hours is likely to change from year to year though.

While the temptation is to suggest that we ought to worry about the amount of sunshine having a realistic impact on temperature, the evidence is that in this context, the differences in latitude and altitude are more important.

What this shows is that (for this data) the amount of Sun is related to the Lat and Height variables somehow.

11.4 Added-Variable Plot (Partial Regression Plot)

Recall that for a simple linear model we can interpret the relationship between Y and \(x\) by drawing a graph - indeed you should always look at a fitted line plot, and possibly a scatterplot with a lowess line as well. The slope that shows up on the fitted line plot exactly matches that which is given in the Regression output.

However for a multiple regression, as we have seen, the regression parameters are usually different to what you get with a simple regression, and so the fitted line plot is no help with visualising the relationship between Y and \(x_1\) or between Y and \(x_2\) (etc.). This is where the Added-variable plot (or “Partial Regression Plot”) comes in.

This plot is based on the idea that if we want to visualise \(\hat{\beta}_{Sun}\) we subtract out all the information provided by the other variable/variables in the model from Lat and Height in this case). Then we plot the residual information in Y against the residual information in Sun.

This gives what can be thought of as a “pure” Sun effect’, i.e. a contribution coming only from Sun and not expressed by the other two variables.

Specifically (using a more general notation) let the explanatory variables be written as \(X_1,…., X_i, ...,X_p\) and we suppose we want to visualise the graph corresponding to regression coefficient \(\hat\beta_i\)

  1. We regress Y against all the predictors except \(X_i\) i.e. regress Y vs \(x_1,...x_{i-1},x_{i+1},...X_p\). Save the residuals e. These residuals represent the information in Y which is not explained by any of the other variables.

  2. Now also regress \(X_i\) against \(x_1,...x_{i-1},x_{x+1},...x_p\). Save the residuals f.

These residuals represent the information in \(x_i\) not contained in any other variable.

  1. Now plot e against f. Any trend in the plot can be thought of as a “pure” Y vs \(x_i\) relationship. In particular, a fitted line plot of e against f will produce a graph with exactly the same slope as in the full regression model. (i.e. with Y predicted by all the regression variables at once.)

A frequent benefit of doing this plot is that it may show that a ‘significant’ predictor is in fact only significant because of an outlier in \(X_i\) or Y. The outlier may not show up as being unusual when the raw \(X_i\) value was plotted against Y. However in relation to other variables it does show up as an outlier. In this circumstance you may decide to delete the outlier and refit the model, in order to see whether the ‘added variable’ \(X_i\) is really needed.

11.4.1 Example

We fitted a model with just Lat and Height a couple of lectures back. It was:

Climate.lm3 = lm(MnJlyTemp ~ Lat + Height, data = Climate)
Climate.lm3 |>
    tidy() |>
    kable()
term estimate std.error statistic p.value
(Intercept) 32.8788366 2.4333203 13.511923 0
Lat -0.6005121 0.0596687 -10.064098 0
Height -0.0071984 0.0009542 -7.543891 0

We will need the residuals from this model and the model using Sun as the response variable.

Climate.lm4 = lm(Sun ~ Lat + Height, data = Climate)
Climate.lm4 |>
    tidy() |>
    kable()
term estimate std.error statistic p.value
(Intercept) 2948.1923582 440.6338786 6.690798 0.0000001
Lat -23.0044035 10.8050185 -2.129048 0.0408019
Height -0.2042485 0.1727897 -1.182064 0.2456282 
e = resid(Climate.lm3)
f = resid(Climate.lm4)
plot(e ~ f)
lines(lowess(f, e))  # note the ordering there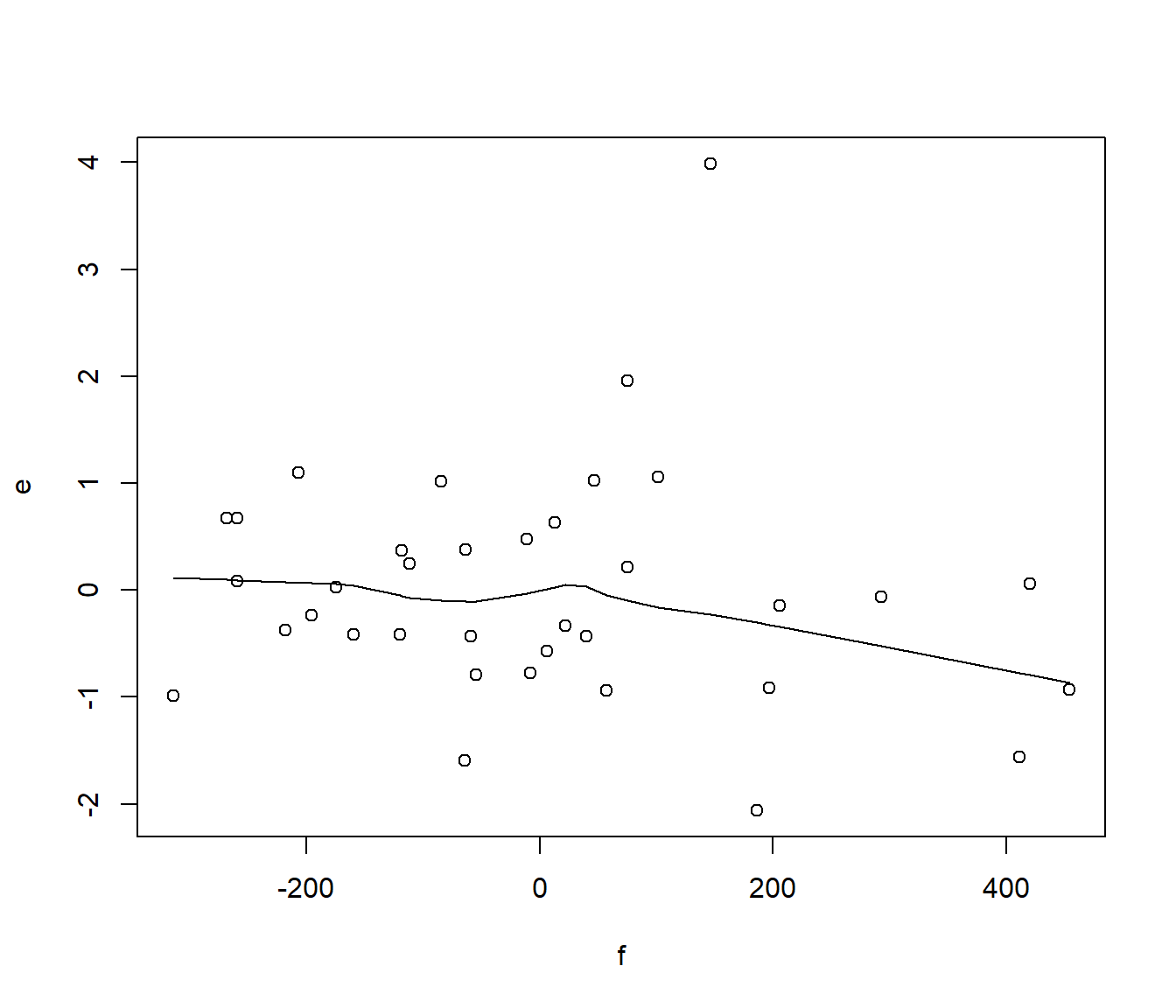
unlabelled

Figure 11.1: Partial Regression Plot for MnJlyTemp against Sun, adjusting for Lat and Height. 

coef(lm(e ~ f))
  (Intercept)             f 
 2.101067e-17 -6.513645e-04

11.4.2 Interpreting the Correlation and \(R^2\) from an Added Variable Plot.

Usefully, if we calculate a correlation R, or the \(R^2\) from the regression of e on f, then these are also interpretable.

11.4.3 Partial correlation

The correlation of the two sets of residuals e and f represent how closely related Y and \(X_i\) are once one adjusts both variables for the effect of the other covariates \(X_1,...,X_{i-1},X_{i+1},...,X_p\). This is called the Partial correlation.

cor.test(e, f)

    Pearson's product-moment correlation

data:  e and f
t = -0.6926, df = 34, p-value = 0.4933
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.4298306  0.2190738
sample estimates:
       cor 
-0.1179513

11.4.4 Partial \(R^2\)

Since e is the residuals after regressing Y on \(x_1,...x_{i-1},x_{x+1},...X_p\) then it represents the variation in Y not explained by the rest of the predictors. Therefore, when we regress the residuals e on f we get an \(R^2\) which is the proportion of previously unexplained variation which is now explained (i.e. it shows the additional benefit of the extra variable).

names(summary(lm(e ~ f)))
 [1] "call"          "terms"         "residuals"     "coefficients" 
 [5] "aliased"       "sigma"         "df"            "r.squared"    
 [9] "adj.r.squared" "fstatistic"    "cov.unscaled" 
summary(lm(e ~ f))$r.squared
[1] 0.01391251
summary(Climate.lm3)$r.squared
[1] 0.8467109

For the regression of mean July temperature on Lat and Height, the \(R^2\) was 84.7%.

Given we saw that Sun was not significant once added to the model with Lat and Height`, we ought to expect only a small increase in \(R^2\). It was 84.9%, found using:

summary(Climate.lm6)$r.squared
[1] 0.8488436

11.4.5 Important things that changed

The adjustment for other variables caused the coefficient for Sun to change, but equally importantly, the standard error for Sun also changed. It is the combination of these changes that will show the impact of the adjustment for other predictors.

Adding variables can make a variable either more important or less important. The t test and p-value are only going to remain unchanged in an extremely specific scenario which is almost impossible for observational study data.

11.5 Optional Task: Hospital Maintenance Data

Data are from 12 naval hospitals in the USA. Response variable, ManHours , is monthly man-hours associated with maintaining the anaesthesiology service. Explanatory variables are

Variable Description
Cases The number of surgical cases
Eligible the eligible population per thousand
OpRooms the number of operating rooms

doctors at play

Source: A Handbook of Small Data Sets by Hand, Daly, Lunn, McConway and Ostrowski.

11.5.1 R output

Download hospital.csv

## Hospital <- read.csv(file = "https://r-resources.massey.ac.nz/161221/data/hospital.csv",
##     header = TRUE)
Hospital.lm <- lm(ManHours ~ ., data = Hospital)
summary(Hospital.lm)

Call:
lm(formula = ManHours ~ ., data = Hospital)

Residuals:
     Min       1Q   Median       3Q      Max 
-218.669  -98.962   -3.585  112.429  195.408 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)  
(Intercept) -114.5895   130.3392  -0.879   0.4049  
Cases          2.0315     0.6778   2.997   0.0171 *
Eligible       2.2714     1.6820   1.350   0.2138  
OpRooms       99.7254    42.2158   2.362   0.0458 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 165.5 on 8 degrees of freedom
Multiple R-squared:  0.9855,    Adjusted R-squared:   0.98 
F-statistic:   181 on 3 and 8 DF,  p-value: 1.087e-07

11.5.2 Questions

  1. Is ManHours related to at least one of the explanatory variables?

  2. Does Cases provide additional information about ManHours when the other explanatory variables are taken into account?

  3. Does Eligible provide additional information about ManHours when the other explanatory variables are taken into account?

  4. Is ManHours related to Eligible?

To understand more about these data, look at scatter plots of the response against each of the explanatory variables.

11.6 Summary for Tests for a Single Predictor

T-tests can be used to test single parameters, and hence assess the importance of single variables in a multiple linear regression model.

The interpretation of these tests depends on what other variables are included in the model.

To test the importance of groups of multiple covariates requires F tests, using the type of technology that was introduced in the previous lecture.