Lecture 10 Testing in Multiple Regression Models (1)
In a multiple regression model there are a variety of hypotheses that we might wish to test. For example:
- Is the mean response related to any of the predictors?
- Does a given predictor provide additional information about the response over and above that provided by the other predictors?
In this lecture we shall look at the methodology for testing question 1 above.
10.1 The F Test for Overall Fit of a Multiple Regression Model
For any given model: \(Y_i = \beta_0 + \beta_1 x_{i1} + \ldots + \beta_p x_{ip} + \varepsilon_i\) where i=1,2,…,n.
We ask: Is the mean response (linearly) related to any of the predictors?
We test:
H0: \(\beta_1 = \beta_2 = \ldots = \beta_p = 0\) i.e. mean response is not linearly related to any of the predictors
against
H1: \(\beta_1, \beta_2, \ldots, \beta_p~\mbox{not all zero}\) i.e. mean response is linearly related to at least one of the predictors.
Testing H0 versus H1 is equivalent to comparing two different models:
M0: \(Y_i = \beta_0 + \varepsilon_i\) and
M1: \(Y_i = \beta_0 + \beta_1 x_{i1} + \ldots + \beta_p x_{ip} + \varepsilon_i\) where i=1,2,…,n.
Model M0 corresponds to H0; Model M1 corresponds to H1.
10.2 General Thoughts on Choosing Between Models
In choosing between models, statisticians have two aims:
- to choose a simple (i.e. not too complex) model;
- to choose a model that fits the data well.
We can measure the complexity of a linear regression model by the number of regression parameters, p+1. The greater this value, the more complex the model.
We can measure the closeness of fit of the model to data using the residual sum of squares.
Think of model comparison like clothes shopping — is it worth spending more (parameters) in order to get a better (model) fit?
10.3 F-Tests for Overall Fit (again)
We want to compare:
Model M0 — cheap (just 1 regression parameter) but may fit badly (residual sum of squares, RSSM0, may be large).
Model M1 — more expensive (p+1 regression parameters) but will fit better (residual sum of squares, RSSM1, smaller).
So we calculate residual sum of squares (RSS) for each model and compute the following F test statistic:
\[F = \frac{[RSS_{M0} - RSS_{M1}]/p}{RSS_{M1}/(n-p-1)}\]
- Intuitively, this F statistic measures (a standardised version of) improvement in fit per “unit cost” (i.e. per extra parameter).
Large values of F suggests that we should prefer M1 to M0. Intuitively, improvement in fit of model is worth the cost.
How large is “large”?
If model M0 is correct (i.e. H0 is correct) then the F test statistic has an F distribution with p,(n-p-1) degrees of freedom, often denoted Fp,n-p-1.
We use these facts to calculate the P-value for the F statistic, and hence test H0 versus H1.
10.4 Aside: The F Distribution
An F distribution is defined by two degrees of freedom.
Random variables from the F distribution take only non-negative values.
Some examples of the density of various F distributions are displayed. The shape depends on the numerator and denominator degrees of freedom…
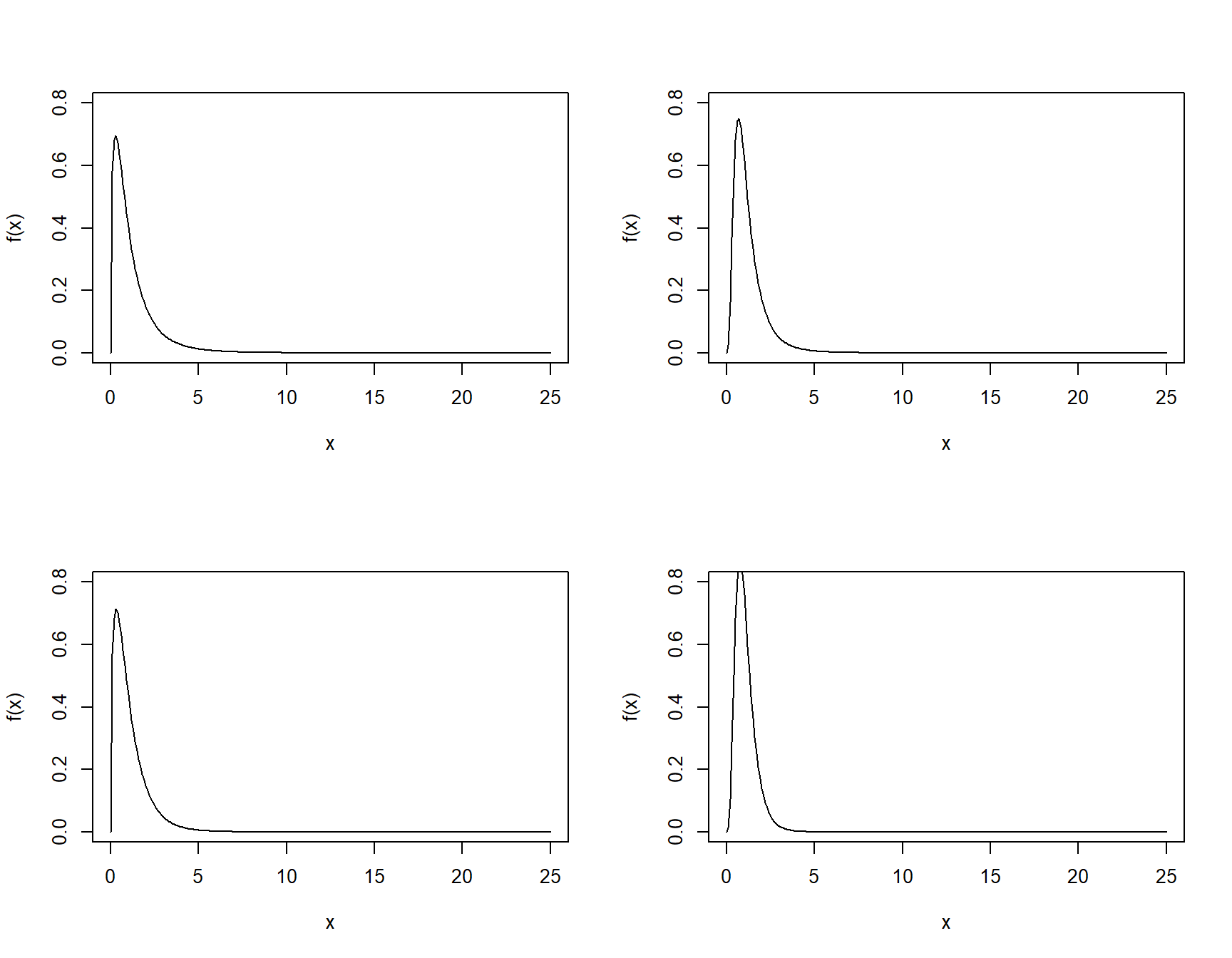
Figure 10.1: Probability density functions for F distributions with numerator df of 3 (left) and 10 (right), and denominator df of (10 (upper) and 30 (lower)
… but large values of x are always unlikely to be observed by chance alone.
As a rough guide, the median of an F distribution is always <1. So if you get an F value less than one, then it is not going to be significant.
If you get an F value greater than ten it definitely is very significant.
10.5 ANOVA table
In most Statistical programs (but not R) it is common to represent the result of a regression with an Analysis of Variance table. It is a useful way to keep track of things. (We’ll soon see how R summarises this table.)
| Source | Sum of squares | df | Mean Square | F |
|---|---|---|---|---|
| Regression | \(SS_{regn}\) | p | \(MS_{regn} = \frac{SS_{regn}}{p}\) | F=\(\frac{MS_{regn}}{MS_{resid}}\) |
| Residuals | \(SS_{resid}\) | n-p-1 | \(MS_{resid}=\frac{SS_{resid} }{n-p-1}\) | |
| Total | \(SS_{Tot}\) | n-1 |
where \(MS_{total} = \sum( Y -\bar Y)^2\), \(~~MS_{error} = \sum( Y -\hat Y)^2\) , p= number of regression parameters (predictors, not including the intercept) the model formula and \(n-p-1\) is the residual df.
Note the First two SS add up to the total SS. So this illustrates how regression separates the different sources of variation or “analyses the variance”.
The df add up as well: p + n-p-1= n-1.
The F is the ratio of the Mean Squared errors.
10.5.1 Analysis of Variance table for Climate data
N.B. Download Climate.csv to be able to run the examples below.
For the climate data we have
Climate = read.csv(file = "../../data/Climate.csv", header = TRUE, row.names = 1)
Climate.lm0 = lm(MnJlyTemp ~ 1, data = Climate)
Climate.lm1 = lm(MnJlyTemp ~ ., data = Climate)
anova(Climate.lm0, Climate.lm1)Analysis of Variance Table
Model 1: MnJlyTemp ~ 1
Model 2: MnJlyTemp ~ Lat + Long + MnJanTemp + Rain + Sun + Height + Sea +
NorthIsland
Res.Df RSS Df Sum of Sq F Pr(>F)
1 35 270.330
2 27 25.022 8 245.31 33.087 5.255e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Note that we have explicitly created the null model Climate.lm0 with no predictor variables.
The use of the anova() command has compared two models here. We show that this way of using anova() is unnecessary below, but we do make frequent use of the anova() command with reference to two (or more) models a lot when working with regression models.
10.6 Omnibus F Test Statistics in R
The above test of whether the response is related to any of the explanatory variables is sometimes called an omnibus F test, while others refer to it as a test of model utility.
We do not have to do the test by hand, or by fitting the null model because R provides the F statistic
and corresponding P-value for this test as a standard part of the
summary() output for a linear model.
10.6.1 Back to Climate example
Call:
lm(formula = MnJlyTemp ~ ., data = Climate)
Residuals:
Min 1Q Median 3Q Max
-1.2213 -0.5257 -0.2620 0.3796 3.3033
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.2829167 24.0200695 0.220 0.82757
Lat -0.3655501 0.1638323 -2.231 0.03416 *
Long 0.1012667 0.1253184 0.808 0.42611
MnJanTemp -0.0380083 0.2901840 -0.131 0.89676
Rain 0.0002901 0.0002971 0.977 0.33744
Sun -0.0006941 0.0011596 -0.599 0.55442
Height -0.0049986 0.0014557 -3.434 0.00194 **
Sea 1.7298287 0.5472228 3.161 0.00386 **
NorthIsland 1.3589549 0.8087868 1.680 0.10445
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9627 on 27 degrees of freedom
Multiple R-squared: 0.9074, Adjusted R-squared: 0.88
F-statistic: 33.09 on 8 and 27 DF, p-value: 5.255e-12 [1] "call" "terms" "residuals" "coefficients"
[5] "aliased" "sigma" "df" "r.squared"
[9] "adj.r.squared" "fstatistic" "cov.unscaled" [1] 0.9074375 value numdf dendf
33.08687 8.00000 27.00000 These figures are the same as were seen earlier when we used the anova() command.