Lecture 30 Weighted regression

In class version

30.1 Introduction

• Weighting by sample size.
• Interpretation of output.
• Weighting to counter heteroscedasticity.

The key idea in this topic is that not all datapoints in the dataset need have the same information value. Some data rows may contain very precise data, while data in the other rows may be less precise.

We therefore adjust our regression analysis to give more “weight” to those datapoints which are more reliable or informative.

30.2 Weighting by Sample Size

The CPS5 dataset is famous in econometrics, referred to often in the book “Introductory Econometrics” by Goldberger.

The dataset has individual-level data on 528 employees EDucation level, whether or not they are in the SOuth of the United States, BL=whether the person was non-white and non-Hispanic 1, otherwise 0, HP= whether or not the person was Hispanic, whether or not the employee was FEmale, years of work EXperience, MS= marital status (1=married, 0 not), whether or not they are members of a UNion, and WG=hourly wage.

Goldberger begins his text by calculating the average WG value for individuals at the various levels of education. (6 years to 18 years of education). Note that most people had 12, 14 or 16 years of education, corresponding to high-school graduates, college graduates and university graduates respectively.

Goldberger then regresses the average WG on ED.

30.3

Download CPS5grouped.csv

## CPS5grouped = read.csv("CPS5grouped.csv", header = TRUE)
CPS5grouped

   EDgroup  AvWage  SEMean   StDev   N
1        6  4.4567 0.79805 1.38226   3
2        7  5.7700 0.83690 1.87136   5
3        8  5.9787 0.62779 2.43142  15
4        9  7.3317 1.29904 4.50000  12
5       10  7.3182 0.64444 2.65711  17
6       11  6.5844 0.64084 3.32992  27
7       12  7.8182 0.25206 3.72159 218
8       13  7.8351 0.66765 4.06114  37
9       14 11.0223 0.92157 6.89643  56
10      15 10.6738 1.39739 5.03837  13
11      16 10.8361 0.63981 5.35304  70
12      17 13.6150 1.42417 6.97699  24
13      18 13.5310 1.09328 6.08715  31

30.4

ggplot(data = CPS5grouped, mapping = aes(x = EDgroup, y = AvWage)) + geom_point(mapping = aes(size = N)) +
    geom_smooth(method = "lm") + labs(x = "Education (hours)", y = "Average wage ($)")

30.5

The data appears to be quite close to the line, which often happens when we have data which have been averaged. The regression suggests we have a high \(R^2 >0.9\).

grouped.lm <- lm(AvWage ~ EDgroup, data = CPS5grouped)
summary(grouped.lm)

Call:
lm(formula = AvWage ~ EDgroup, data = CPS5grouped)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.5637 -0.7350  0.1266  0.7158  1.3198 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.01445    0.87462  -0.017    0.987    
EDgroup      0.72410    0.06958  10.406 4.96e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9387 on 11 degrees of freedom
Multiple R-squared:  0.9078,    Adjusted R-squared:  0.8994 
F-statistic: 108.3 on 1 and 11 DF,  p-value: 4.958e-07

30.6

However note that the left-hand points represent only a few individuals compared to some of the right-hand points, represented by the size of the circles scaling with the number of individuals \(N\) contributing to the average. We would like the regression line to be closer to those points that represent far more people.

The line is close to the first category (which has only three people in it) and far from the 12, 14, 16-year categories which have the most people. This doesn’t really make sense.

If we use the ungrouped data the relationship between Wage and Education is much weaker in terms of goodness of fit of the model.

30.7

Download CPS5.csv

## CPS5 = read.csv("CPS5.csv", header = TRUE)
head(CPS5)

  ED SO BL HP FE MS EX UN   WG
1 10  0  0  0  0  1 27  0  9.0
2 12  0  0  0  0  1 20  0  5.5
3 12  0  0  0  1  0  4  0  3.8
4 12  0  0  0  1  1 29  0 10.5
5 12  0  0  0  0  1 40  1 15.0
6 16  0  0  0  1  1 27  0  9.0

30.8

ggplot(data = CPS5, mapping = aes(x = ED, y = WG)) + geom_point() + geom_smooth(method = "lm") +
    labs(x = "Education (years)", y = "Wage ($)")

`geom_smooth()` using formula = 'y ~ x'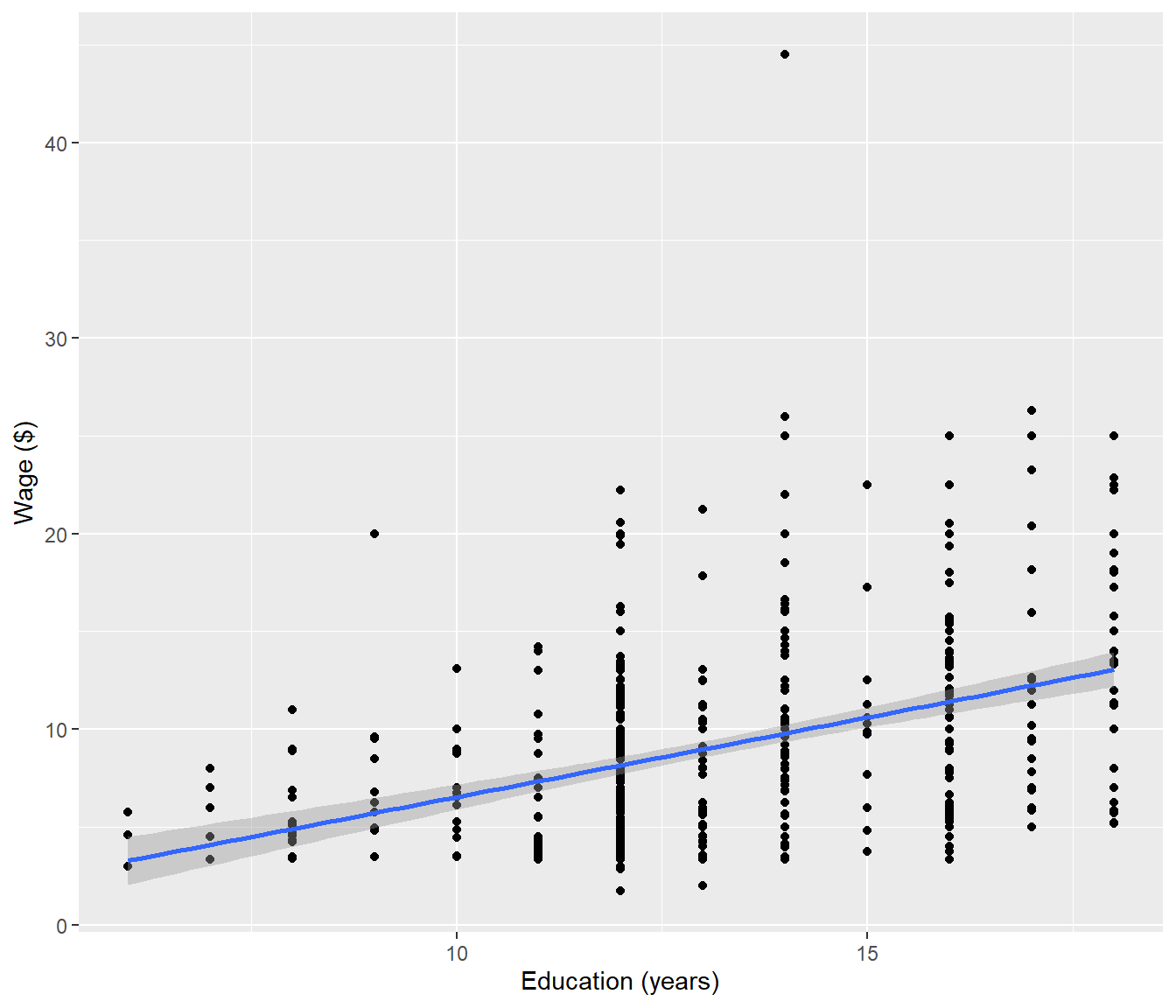

30.9

cps5.lm = lm(WG ~ ED, data = CPS5)
summary(cps5.lm)

Call:
lm(formula = WG ~ ED, data = CPS5)

Residuals:
   Min     1Q Median     3Q    Max 
-8.068 -3.163 -0.700  2.289 34.709 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.60468    1.10318  -1.455    0.146    
ED           0.81395    0.08281   9.829   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.733 on 526 degrees of freedom
Multiple R-squared:  0.1552,    Adjusted R-squared:  0.1536 
F-statistic:  96.6 on 1 and 526 DF,  p-value: < 2.2e-16

We see there is an outlier, which could be a typo (decimal point in the wrong place?) However the main focus here is that there is a lot more variation among the individual data than there is among the averaged data, so the \(R^2\) is much lower. Also the regression coefficients have different values.

30.10 Why Grouped Regression Results Differ

Formulas not examinable but conclusion is important.

To explain the difference between these two regressions, we consider the regression of \(Y\) vs \(X\) (\(n\) data) and \(\bar Y\) versus \(\bar X\) (where the data have been divided into \(m\) groups - a much smaller number than \(n\).) In Least Squares we choose \(\beta_0\) and \(\beta_1\) to minimise
\[SS_{error} = \sum^n_{i=1}(y_i - \beta_0- \beta_1 x_i)^2 ~~~~ (1) \] However the regression for the averages treats all \(m\) groups as being of equal worth: \[ \sum^m_{j=1}(\bar y_j - \beta_0- \beta_1 \bar x_j)^2 ~~~~~~ (2) \]
That is, the computations will try just as hard to fit a value that arises from a small group of data as a value from a large group.

30.11 How are these two sums of squares related?

If we take the sum in (1) and re-order it into Education level groups we get \[SS_{error} = \sum^m_{j=1}\sum^{n_j}_{i=1}(y_{ij} - \beta_0- \beta_1 x_{ij})^2 ~~~~ (3) \]

Now suppose for a moment we pretend that all the \(y_{ij}\) values are the same as the group mean \(\bar y_j\) (and note that already \(x_{ij} = \bar x_j\) ). Then the sum on the right-hand side reduces to \[SS_{error} = \sum^m_{j=1} n_j(\bar y_{ j} - \beta_0 - \beta_1 \bar x_j)^2 ~~~~ (4) \]

So the difference between this sum and the sum (2) is that the squared residual is multiplied by \(n_j\), the number of people in that group. We call this multiplier the weight \(w_j\).

Essentially we interpret the weight as the amount of information represented by the datapoint. So here in this simple example “amount of information” is easily measured as the sample size \(w_j = n_j\) at each education level.

30.12

But in fact we don’t have all the \(y_{ij}\) equal. Instead what we do is to add and subtract \(\bar y_j\) inside the parentheses in equation (3), and then expand the square: \[\begin{aligned}SS_{error} &= \sum^m_{j=1}\sum^{n_j}_{i=1}(y_{ij} -\bar y_j + \bar y_j - \beta_0- \beta_1 x_{ij})^2\\&= \sum^m_{j=1}\sum^{n_j}_{i=1}(y_{ij} -\bar y_j)^2 + \sum^m_{j=1}\sum^{n_j}_{i=1}(\bar y_j - \beta_0- \beta_1 \bar x_j)^2 ~~~~~(*)\\&= \sum^m_{j=1}\sum^{n_j}_{i=1}(y_{ij} -\bar y_j)^2 + \sum^m_{j=1} n_j~(\bar y_j - \beta_0- \beta_1 \bar x_j)^2\end{aligned}\]

(*) Equality happens because the cross-product term \(\sum^m_{j=1} \sum^{n_j}_{i=1} ~2~(y_{ij} -\bar y_j) (\bar y_j - \beta_0- \beta_1 \bar x_j) =0\).

30.13

The key fact is that the error SS splits into two parts:

\[SS_{error} = \sum^m_{j=1}\sum^{n_j}_{i=1}(y_{ij} -\bar y_j)^2 + \sum^m_{j=1} n_j~(\bar y_j - \beta_0- \beta_1 \bar x_j)^2\] - The first term is the “pure error” SS for \(y_{ij}\) and relates to the variation in the \(y_{ij}\)s around the group means \(\bar y_j\), and

• the second term is the weighted SS that one gets from pretending all the \(y_{ij}\)s occur at \(\bar y_j\) .

Note that estimation of \(\beta_0\) and \(\beta_1\) depends only on the second term. Therefore the regression coefficients you get from weighted regression should be exactly the same as those from handling the whole data.

However the estimate of goodness of fit (\(R^2\)) would be entirely wrong as the variance is underestimated (missing the first term).

30.14 Weighted regression in R

To do a weighted regression we have to specify weights in the lm() command. Below we compare the weighted least squares (WLS) estimates from the averaged data to the ungrouped ordinary least squares (OLS) estimates from the raw data.

cps.wls = lm(AvWage ~ EDgroup, weights = N, data = CPS5grouped)
summary(cps.wls)

Call:
lm(formula = AvWage ~ EDgroup, data = CPS5grouped, weights = N)

Weighted Residuals:
   Min     1Q Median     3Q    Max 
-6.944 -3.971  2.699  4.151  9.217 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.60468    1.27442  -1.259    0.234    
EDgroup      0.81395    0.09567   8.508 3.62e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.467 on 11 degrees of freedom
Multiple R-squared:  0.8681,    Adjusted R-squared:  0.8561 
F-statistic: 72.39 on 1 and 11 DF,  p-value: 3.621e-06

30.15

summary(cps5.lm)

Call:
lm(formula = WG ~ ED, data = CPS5)

Residuals:
   Min     1Q Median     3Q    Max 
-8.068 -3.163 -0.700  2.289 34.709 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.60468    1.10318  -1.455    0.146    
ED           0.81395    0.08281   9.829   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.733 on 526 degrees of freedom
Multiple R-squared:  0.1552,    Adjusted R-squared:  0.1536 
F-statistic:  96.6 on 1 and 526 DF,  p-value: < 2.2e-16

We see that the coefficient estimates are the same, but the standard errors and the \(R^2\) are different.

The following plot shows the averaged data with the unweighted (dashed) and weighted (solid red) lines. The weighted line is closer to where more data are.

30.16

ggplot(data = CPS5grouped, mapping = aes(x = AvWage, y = EDgroup)) + geom_point(mapping = aes(size = N)) +
    geom_smooth(method = "lm", mapping = aes(weight = N), col = "red", se = FALSE) +
    geom_smooth(method = "lm", linetype = "dashed", se = FALSE) + labs(x = "Education (years)",
    y = "Average wage ($)")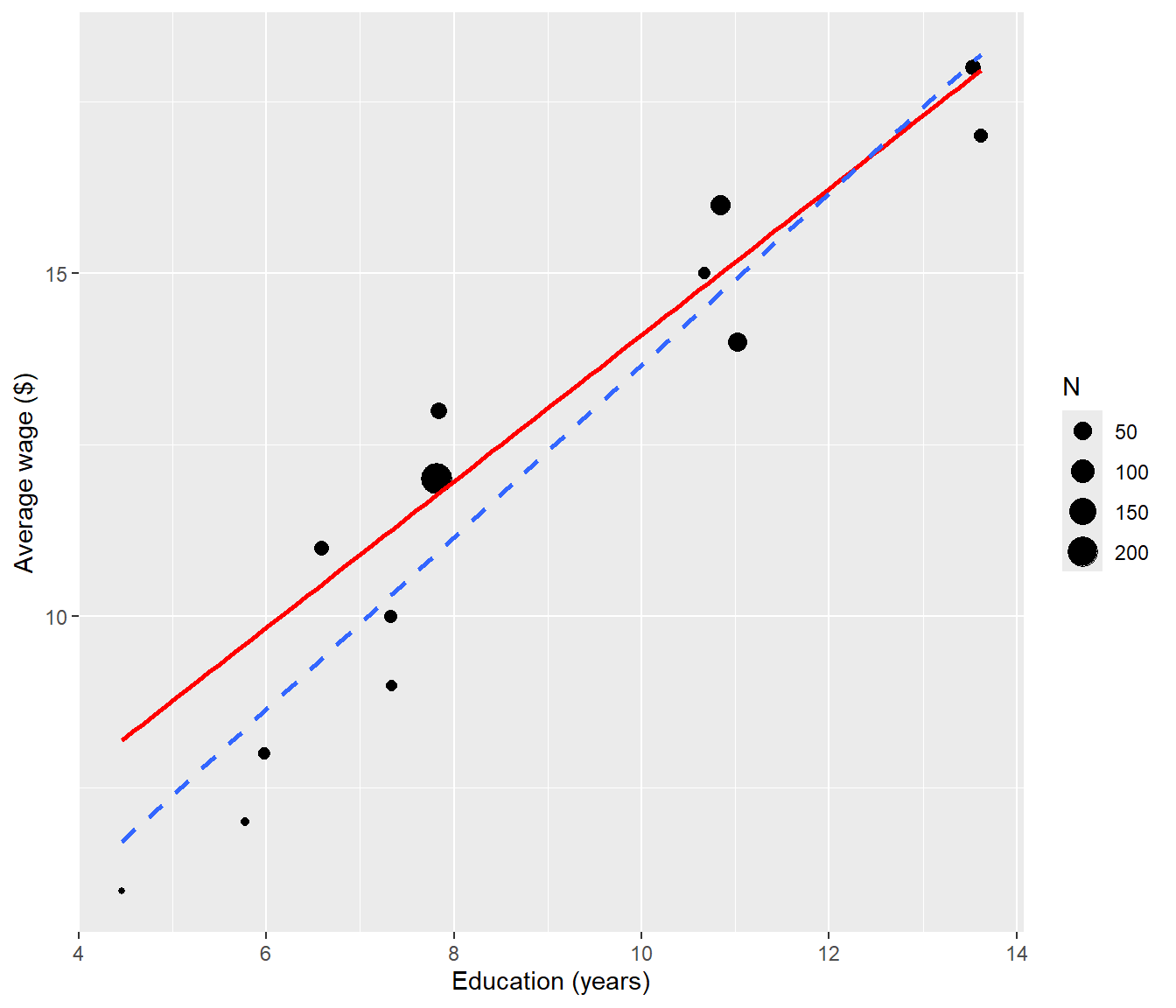

30.17 Residuals for Weighted Regression

Clearly a plot of ordinary residuals could be misleading in the context of weighted least squares. The low weight points on the left are badly fitted and this could make them look like influential outliers.

augment(cps.wls, CPS5grouped) |>
    ggplot(mapping = aes(x = EDgroup, y = .resid)) + geom_point() + geom_hline(yintercept = 0,
    linetype = "dotted") + labs(y = "Simple residuals", x = "Education group (years)")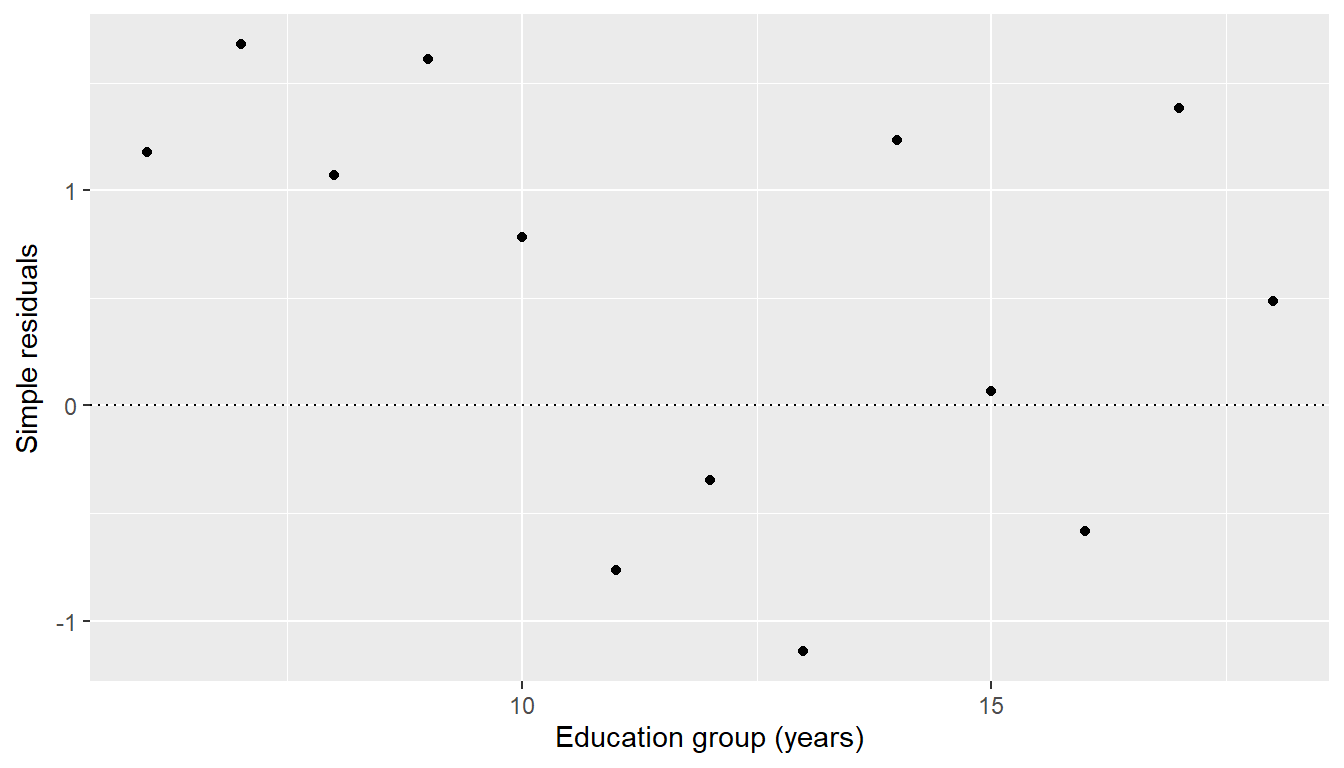

30.18

Instead we use “weighted” or Pearson” Residuals \(r_j = \sqrt{w_j}\varepsilon_j\).

augment(cps.wls, CPS5grouped) |>
    mutate(pearson = .resid * sqrt(N)) |>
    ggplot(mapping = aes(x = EDgroup, y = pearson)) + geom_point() + geom_hline(yintercept = 0,
    linetype = "dotted") + labs(y = "Pearson (weighted) residuals", x = "Education group (years)")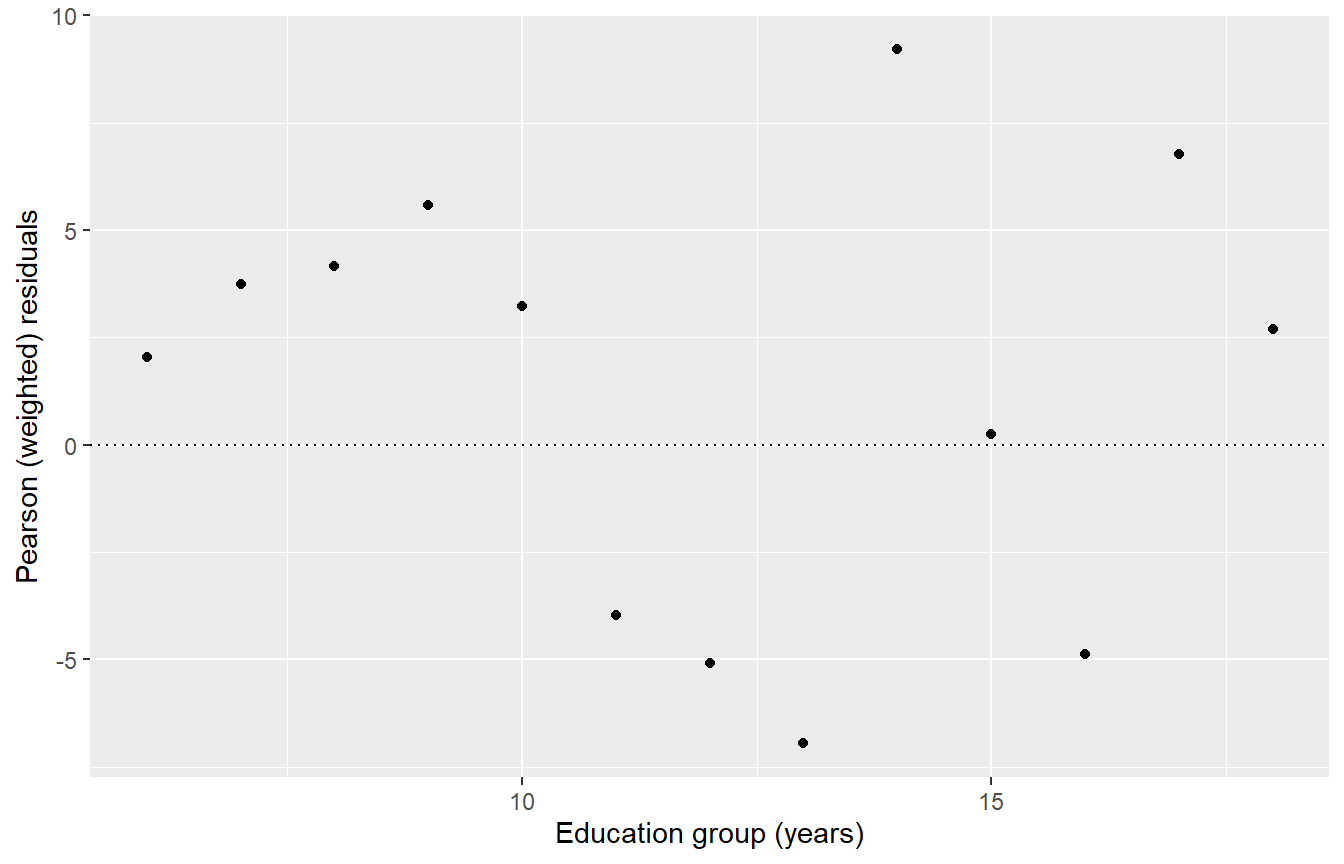

30.19

This has given a proper sense of importance to each residual. We see that the low-weight points on the left are not particularly important.

Unfortunately the \(Y\) axis scale is now meaningless so all we can look at is the shape and the relative importance or lack of fit for each point.

30.20 Weighting For Non-Constant Variance

Suppose we have data for which the variance is non-constant. So we want to give more weight to those points which have small variance (or are known more precisely) and give less weight to those points that have bigger variance (or are known less precisely).

This still fits with the idea that Weight represents the amount of information carried by each datapoint.

30.20.1 Supervisors and Workers

The following data is on the number of supervisors \(Y\) (e.g. team leaders) and the number of workers \(X\) at a number of industrial establishments. The data are from the book by Chatterjee and Price “Regression Analysis by Example”

Download supervisors.csv

## supervisors = read.csv("supervisors.csv")
supervisors

      X   Y
1   294  30
2   247  32
3   267  37
4   358  44
5   423  47
6   311  49
7   450  56
8   534  62
9   438  68
10  697  78
11  688  80
12  630  84
13  709  88
14  627  97
15  615 100
16  999 109
17 1022 114
18 1015 117
19  700 106
20  850 128
21  980 130
22 1025 160
23 1021  97
24 1200 180
25 1250 112
26 1500 210
27 1650 135

30.21

ggplot(supervisors, mapping = aes(x = X, y = Y)) + geom_point() + geom_smooth(method = "lm") +
    labs(x = "Number of workers (X)", y = "Number of supervisors (Y)")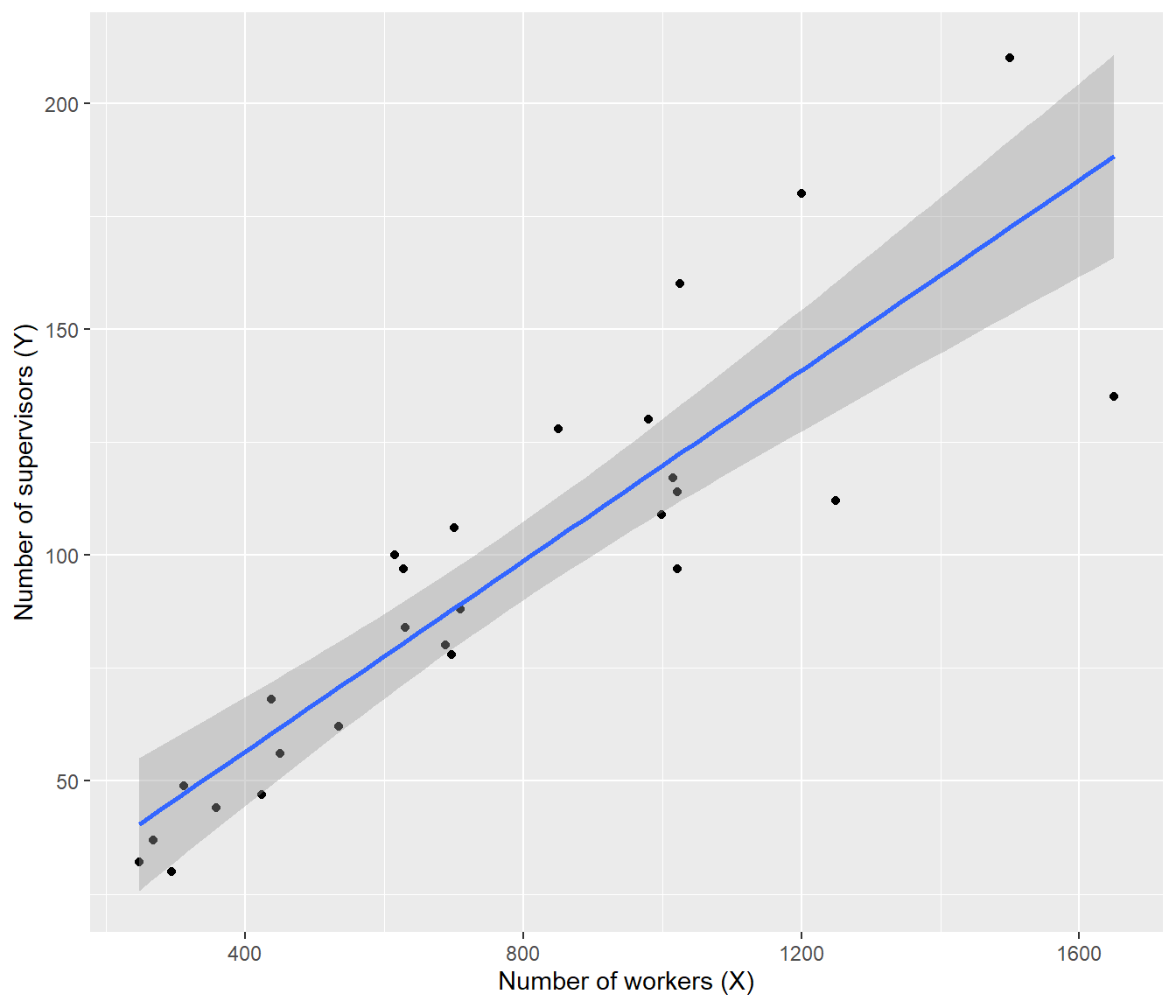

30.22

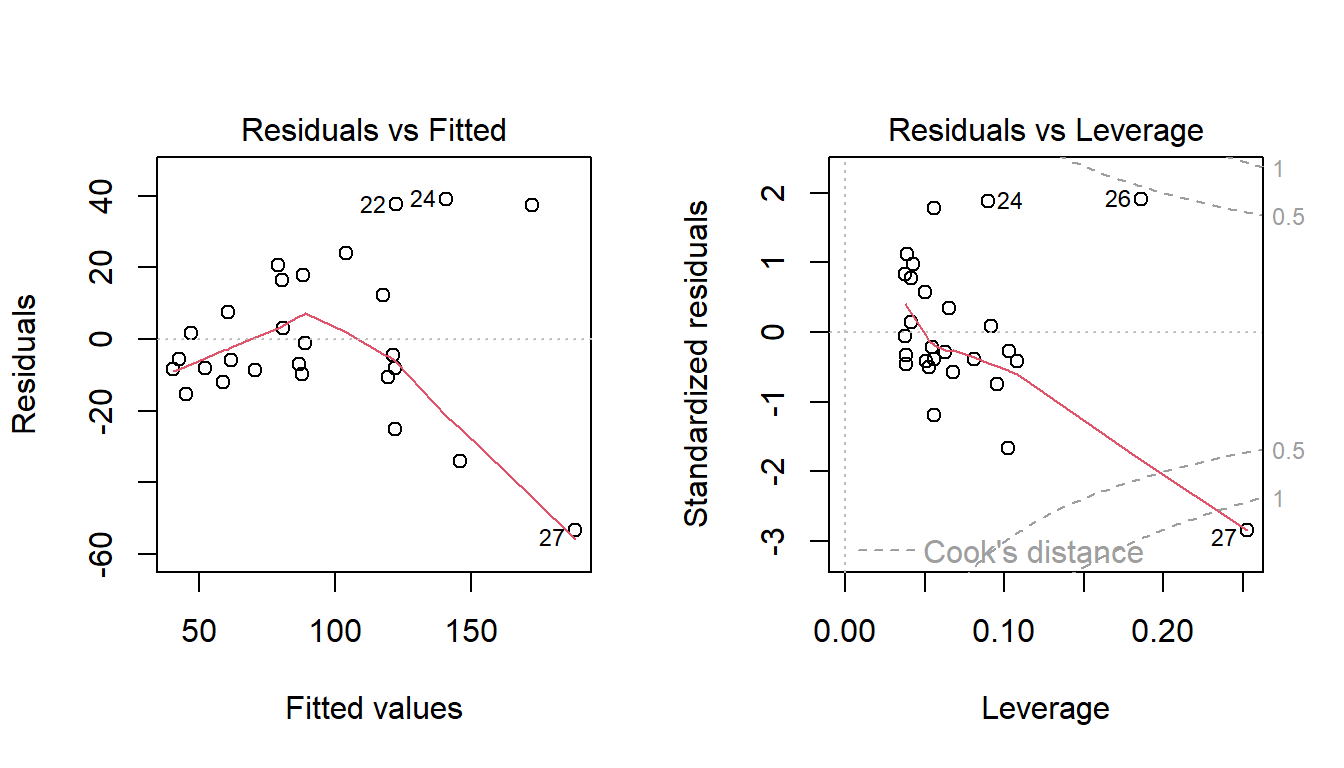
Note that the line is overshooting the cluster of points on the left. The residual plots show curvature and heteroscedasticity. The fourth graph shows a simple linear model is highly influenced by the points at the right, which have very large residuals.

sup.lm <- lm(Y ~ X, data = supervisors)
par(mfrow = c(1, 2))
plot(sup.lm, which = c(1, 5))

30.23

Considering the heteroscedasticity, look at the amount of vertical spread of residuals when \(x\)= 400, 800 and 1600. As \(X\) doubles, the spread roughly doubles. This suggests that \(\mbox{sd}(\varepsilon) \propto x\), or in other words \(\sigma = k x\) for some constant \(k\).

Now let us suppose we want to fit a straight-line model \[y_i = \beta_0 + \beta_1 x_i + \varepsilon_i ~ \] We would ordinarily solve this by minimising the \[SS_{error} = \sum( y_i - \beta_0 - \beta_1 x_i)^2\] where the components of the sum (the residuals \(y_i - \beta_0 - \beta_1 x_i\)) have constant standard deviation. Except now the standard deviation is not constant.

But what we could do is divide through by \(x_i\). The model becomes \[\begin{aligned}\frac{y_i}{x_i} &= \frac{\beta_0}{x_i} + \beta_1\frac{x_i}{x_i} + \frac{\varepsilon_i}{x_i}\\Y_i &=\beta_0 X_i + \beta_1 + \eta_i\end{aligned}\] where \(Y_i = \frac{y_i}{x_i}\), \(X_i = \frac{1}{x_i}\) and \(\eta_i = \frac{\varepsilon_i}{x_i}\).

30.24

The error term \(\eta_i\) now has constant standard deviation as

\[\mbox{sd}\left( \frac{\varepsilon_i}{x_i}\right) = \frac{ kx_i}{x_i} = k.\]

We now have a linear model with constant variance so can solve by least squares in the usual way.

We could do the transformation ourselves and then just use lm() normally, but another way to look at it is we’re minimising

\[\sum \left(\frac{y_i}{x_i} - \frac{\beta_0}{x_i} - \beta_1 \right)^2 ~~= ~~ \sum \frac{1}{x_i^2}\left(y_i - \beta_0 -\beta_1 x_i \right)^2\]

which is a weighted regression with \(w_i = 1/ x_i^2\). So the task with this transformation is the same as weighted least squares with these weights.

30.25

sup.wls = lm(Y ~ X, data = supervisors, weights = 1/X^2)
summary(sup.wls)

Call:
lm(formula = Y ~ X, data = supervisors, weights = 1/X^2)

Weighted Residuals:
      Min        1Q    Median        3Q       Max 
-0.041477 -0.013852 -0.004998  0.024671  0.035427 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3.803296   4.569745   0.832    0.413    
X           0.120990   0.008999  13.445 6.04e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.02266 on 25 degrees of freedom
Multiple R-squared:  0.8785,    Adjusted R-squared:  0.8737 
F-statistic: 180.8 on 1 and 25 DF,  p-value: 6.044e-13

30.26

ggplot(data = supervisors, mapping = aes(x = X, y = Y)) + geom_point() + geom_smooth(method = "lm",
    mapping = aes(weight = 1/X^2), col = "red", se = FALSE) + geom_smooth(method = "lm",
    linetype = "dotted", se = FALSE) + labs(x = "Number of workers (X)", y = "Number of supervisors (Y)")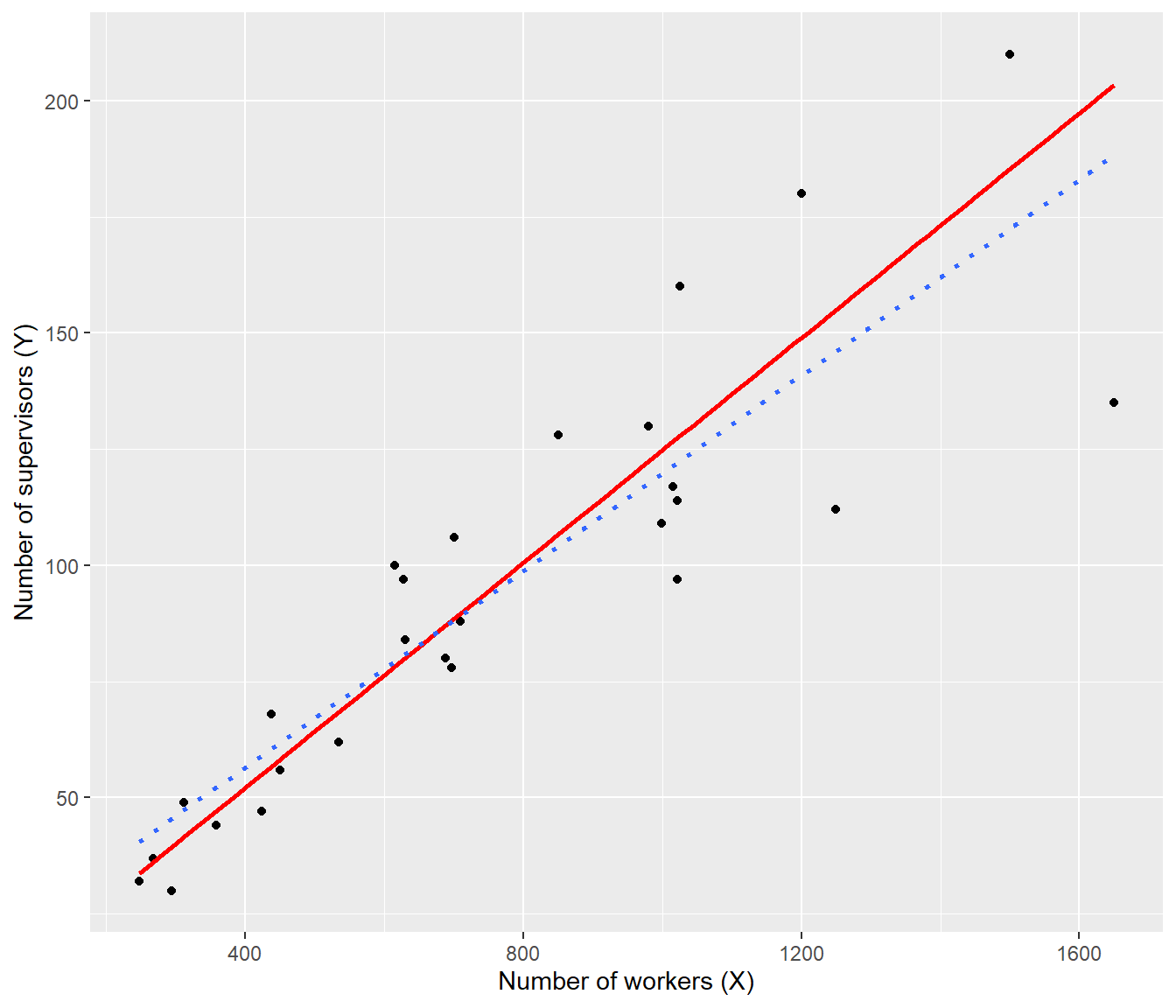

30.27

The plot shows that weighted line (red, solid) is now going closer to the data at the left, where the random error is smallest, whereas the OLS line (dotted) overshot the data at left.

The plot of weighted residuals below shows constant variance (with perhaps a little curvature).

augment(sup.wls) |>
    mutate(pearson = .resid/X) |>
    ggplot(mapping = aes(x = X, y = pearson)) + geom_point() + geom_hline(yintercept = 0,
    linetype = "dotted")

labs(y = "Pearson (weighted) residuals", x = "Number of workers (X)")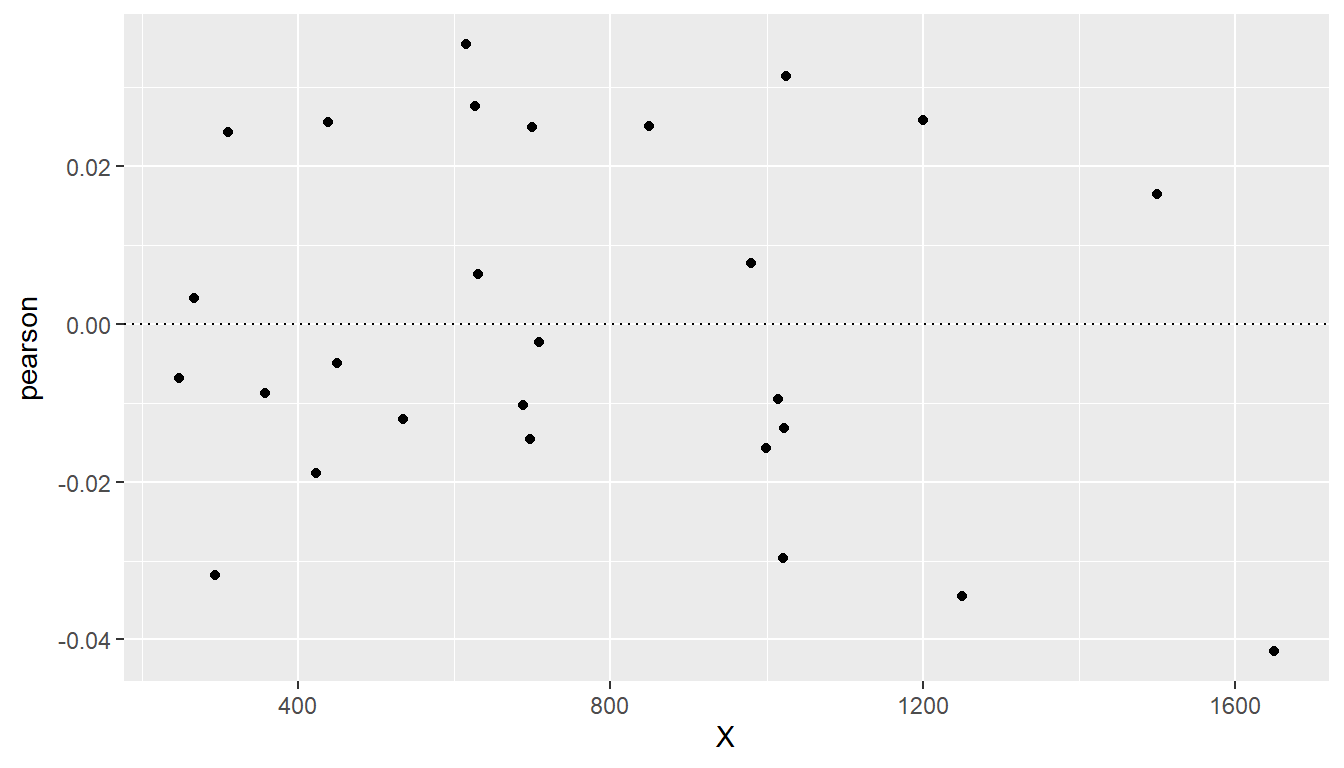

$y
[1] "Pearson (weighted) residuals"

$x
[1] "Number of workers (X)"

attr(,"class")
[1] "labels"

30.28 Basic rule for Weighting

Assume weights \[w_i = \frac{n_i}{\mbox{variance}_i} ~~~~~ (6) \]

where, if \(n\) doesn’t vary between data rows then just replace by \(n=1\), and if the precision of data (1/variance) does not differ between data rows then just drop that term.

30.28.1 Application: Meta Analysis

You may have heard of the field of meta-analysis, which is concerned with combining the results of many small studies in order to get an overall result.

Meta-analysis uses weights of the form (6) to represent the differing amounts and quality of data from the different studies.

30.29 Revisiting the CPS5grouped data

For these data, there was a column of standard deviations (StDev) as well as sample sizes N. So we could use weights \(W_i = N_i/ \mbox{StDev}_i^2\)

CPS5weighted <- CPS5grouped |> mutate(Wt = N/ StDev^2)
cps.wls2 <- lm(AvWage ~ EDgroup, weights=Wt, data=CPS5weighted)
summary(cps.wls2)

Call:
lm(formula = AvWage ~ EDgroup, data = CPS5weighted, weights = Wt)

Weighted Residuals:
    Min      1Q  Median      3Q     Max 
-1.4367  0.1153  0.7399  1.0895  1.7058 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.26605    0.93427   0.285    0.781    
EDgroup      0.65602    0.07828   8.381 4.19e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.21 on 11 degrees of freedom
Multiple R-squared:  0.8646,    Adjusted R-squared:  0.8523 
F-statistic: 70.24 on 1 and 11 DF,  p-value: 4.186e-06

30.30

ggplot(data = CPS5weighted, mapping = aes(x = EDgroup, y = AvWage)) + geom_point(mapping = aes(size = N)) +
    geom_smooth(method = "lm", mapping = aes(weight = Wt), col = "red", se = FALSE) +
    geom_smooth(method = "lm", mapping = aes(weight = N), linetype = "dotted", se = FALSE) +
    labs(x = "Education group (years)", y = "Average Wage ($)")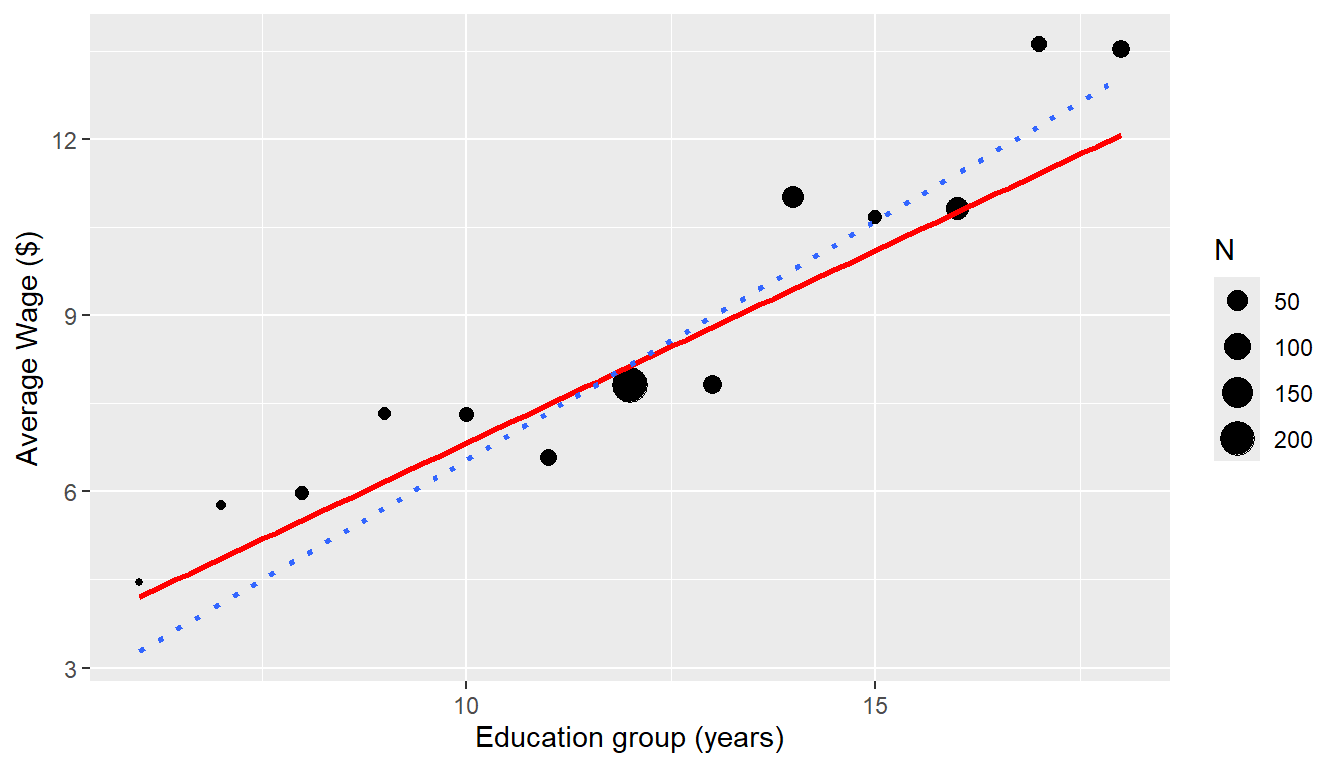

The standard deviations are much higher for the highly-educated groups, so that counteracts some of the effect of higher sample sizes.