Lecture 32 Models with Autoregressive Errors

In class version

32.1

We saw previously that when linear models are fitted to time series data, the residuals can display autocorrelation. The consequences of autocorrelation are that

  • standard errors given by standard least squares theory (and hence by standard R output) will usually be smaller than the true standard deviations of the parameter estimates.

  • the result is that t-test statistics will be inflated, p-values too small, and confidence intervals will be too narrow.

32.2 Accounting for Autocorrelation in the Errors

The consequence of standard errors and p-values being out means that we need to account for autocorrelation in the errors when it is present.

This will require two steps:

  • Definition of an appropriate model for autocorrelated errors;
  • Fitting the linear model with autocorrelated errors.

We now consider modeling the errors using autoregressive models.

32.3 Autoregressive Models

In a time series, the errors \(\varepsilon_1, \varepsilon_2, \ldots, \varepsilon_n\) can be thought of as a realization of a random process (in time).

We can model serial correlation between these errors by making each one explicitly dependent on the previous one: \[\varepsilon_t = \phi \varepsilon_{t-1} + \eta_t\] where \(\eta_t~(t=1,2,\ldots,n)\) is white noise, that is, a sequence of independent and identically distributed (normal) random variables with zero mean.

  • This equation is a first order autoregressive (or AR1) model for \(\varepsilon_t\).
  • Under this model, \(\mbox{Corr}(\varepsilon_t, \varepsilon_{t-1}) = \phi\).
  • Consequently, more generally, \(\mbox{Corr}(\varepsilon_t, \varepsilon_{t-k}) = \phi^k\)

32.4 ACF Plots for AR1 Processes

To illustrate an ACF plot for a function demonstrating autocorrelation, we create two variables from white noise

Z1 = rnorm(1000)
X1 = Z1[-1] + 0.85 * Z1[-1000]
X2 = Z1[-1] - 0.85 * Z1[-1000]
par(mfrow = c(1, 2), mai = rep(0.5, 4))
plot(X1, type = "l")
plot(X2, type = "l")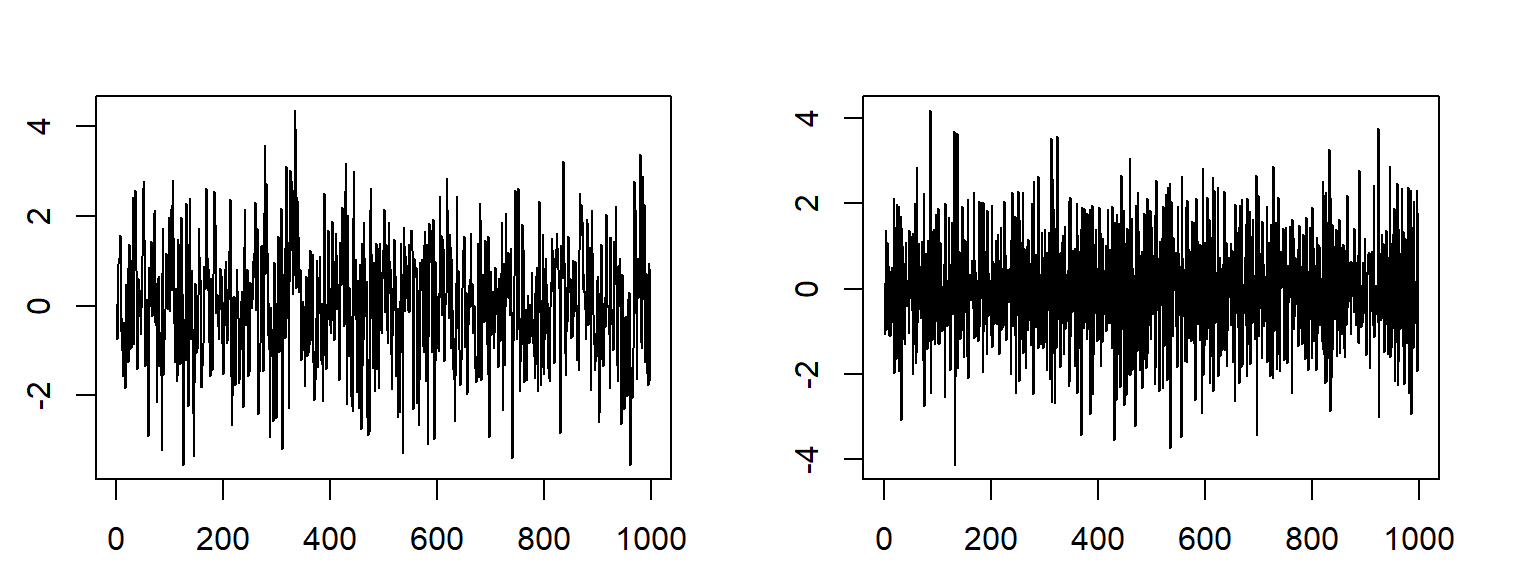

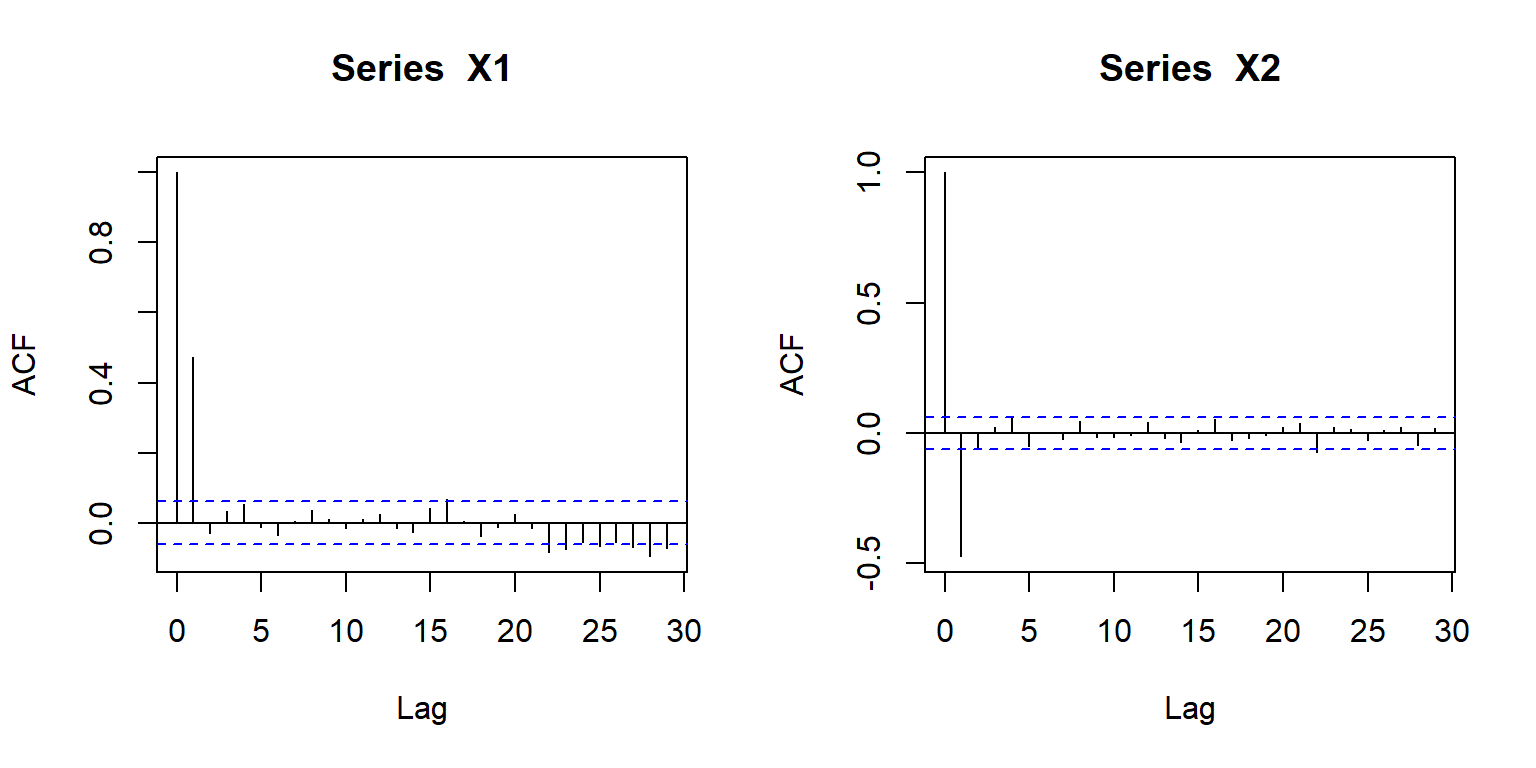
unlabelled

32.5 

par(mfrow = c(1, 2))
acf(X1)
acf(X2)

unlabelled

The X1 series has correlation of 0.472 at lag 1, while the X2 series has autocorrelation of -0.473 at lag1

32.6 Autoregressive Models for Errors in Linear Modelling

If residuals in a linear model for time series data display autocorrelation then we change the model to allow for an AR1 correlation structure for the residuals in our model to account for this.

N.B. More complex models are also possible. For example:

  • AR models of order q>1, where \(\varepsilon_t\) is modelled as explicitly dependent on the previous q errors;
  • moving average (MA) models and autoregressive moving average (ARMA) models.
  • For the purposes of this course we will focus on AR1 models for the error process.

32.7 Application to the Tourism Data

Download motel.csv

## tourism <- read_csv(file = "motel.csv")
tourism <- tourism |>
    mutate(Time = round(time_length(Date - min(Date), unit = "month")), Month = factor(month(Date,
        label = TRUE), ordered = FALSE), Year = year(Date))
tourism
# A tibble: 180 × 6
   Date       RoomNights AvePrice  Time Month  Year
   <date>          <dbl>    <dbl> <dbl> <fct> <dbl>
 1 1980-01-01     276986     27.7     0 Jan    1980
 2 1980-02-01     260633     28.7     1 Feb    1980
 3 1980-03-01     291551     28.6     2 Mar    1980
 4 1980-04-01     275383     28.3     3 Apr    1980
 5 1980-05-01     275302     28.7     4 May    1980
 6 1980-06-01     231693     28.6     5 Jun    1980
 7 1980-07-01     238829     29.2     6 Jul    1980
 8 1980-08-01     274215     29.8     7 Aug    1980
 9 1980-09-01     277808     29.6     8 Sep    1980
10 1980-10-01     299060     30.3     9 Oct    1980
# ℹ 170 more rows

32.8 

tourism.lm <- lm(RoomNights ~ Time + Month, data = tourism)
acf(resid(tourism.lm))

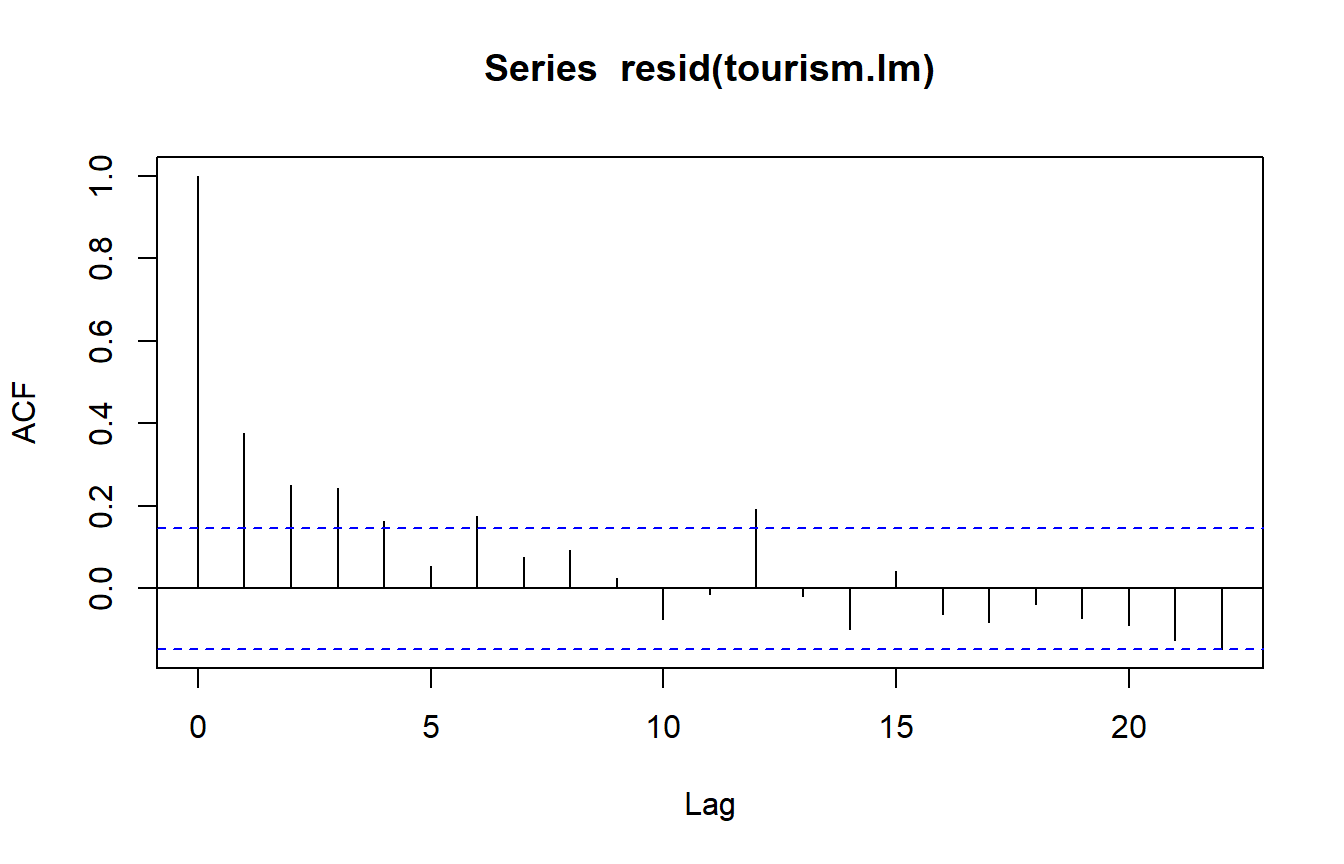
unlabelled

There is a suggestion of exponential decay in autocorrelations. - AR1 model (with positive \(\phi\)) for errors seems reasonable.

32.9

The model incorporating the AR1 error process, and written in regression format, is as follows:

\[\begin{aligned} Y_{t} &= \beta_0 + \beta_1 \mbox{Time} + \beta_2 z_{t,2} + \beta_3 z_{t,3} + \ldots + \beta_{12} z_{t,12} + \varepsilon_t \\ \varepsilon_t &= \phi \varepsilon_{t-1} + \eta_{t}\end{aligned}\]

where:

  • \(Y_t\) is the \(t\)th observation of RoomNights;
  • \(z_{t,j} = 1\) if observation \(t\) is taken in month \(j\);
  • \(z_{t,j} = 0\) otherwise.
  • \(\eta_1, \ldots, \eta_n\) are independent and identically distributed normal random variables with mean zero.

32.10 Model Fitting with Autoregressive Errors

To fit a model with AR1 errors, we must:

  • Estimate the size of the autocorrelation parameter, \(\phi\).
  • Account for the autocorrelation in errors when estimating the regression coefficients.

The AR1 parameter, \(\phi\), can be estimated by the method of (restricted) maximum likelihood.

The details are beyond the scope of this paper, but you will meet maximum likelihood estimation if you take 161.304 or 161.331.

Once \(\phi\) is estimated, we can account for the AR1 nature of the errors by fitting the linear model using generalized least squares.

32.11 Generalized Least Squares

Once we have \(\phi\) estimated, we can then estimate the regression coefficients \(\beta\) by rearranging the regression equation to eliminate the autocorrelation:

Suppose \[ \begin{aligned} y_t &= \beta_0 + \beta_1 x_t + \varepsilon_t\\ \varepsilon_t &= \phi \varepsilon_{t-1} + \eta_t \end{aligned} \] where \(\eta_t \underset{\mathsf{iid}}\sim N(0, 1)\). Then \[ \begin{aligned} y_t - \phi y_{t-1} &= \beta_0 + \beta_1 x_t + \varepsilon_t - \phi (\beta_0 + \beta_1 x_{t-1} + \varepsilon_{t-1})\\ &= \beta_0(1 - \phi) + \beta_1 (x_t - \phi x_{t-1}) + \varepsilon_t - \phi \varepsilon_{t-1}\\ &= \beta_0(1 - \phi) + \beta_1 (x_t - \phi x_{t-1}) + \eta_t \end{aligned} \] which is a standard linear regression in the new variables \(Y_t = y_t - \phi y_{t-1}\), \(X_t = x_t - \phi x_{t-1}\).

Thus we can fit this with least squares. The “generalised” bit is the trick we use to transform something that is not regular least squares to a least squares situation - it turns out we can do this no matter what the covariance structure is among the predictors as long as the structure is estimable from the data.

32.12 Generalized Least Squares in R

In R, linear models can be fitted using this technique using the gls() command found in the nlme add-on package.

Call this package using library(nlme) before using the gls() command.

library(nlme)
  • The gls() command uses the same model formula as lm(), but also accepts an additional argument to describe the correlation structure for the errors.

32.13 Generalized Least Squares and the Tourism Data

tourism.gls <- gls(RoomNights ~ Time + Month, correlation = corAR1(), data = tourism)
anova(tourism.gls)
Denom. DF: 167 
            numDF  F-value p-value
(Intercept)     1 45239.15  <.0001
Time            1  1092.85  <.0001
Month          11    81.94  <.0001

The use of an AR1 error process is obtained by setting correlation=corAR1() in the gls() command.

Both Time and Month are associated with RoomNights (P-value less than \(0.0001\) in both cases).

32.14 

summary(tourism.gls)
Generalized least squares fit by REML
  Model: RoomNights ~ Time + Month 
  Data: tourism 
       AIC      BIC    logLik
  3727.911 3774.681 -1848.955

Correlation Structure: AR(1)
 Formula: ~1 
 Parameter estimate(s):
     Phi 
0.392721 

Coefficients:
                Value Std.Error   t-value p-value
(Intercept) 275492.20  4692.407  58.71021  0.0000
Time          1062.25    31.870  33.33115  0.0000
MonthFeb    -31194.09  4205.044  -7.41825  0.0000
MonthMar     23482.73  4959.531   4.73487  0.0000
MonthApr     -2170.47  5225.494  -0.41536  0.6784
MonthMay    -19419.12  5325.710  -3.64630  0.0004
MonthJun    -65827.11  5362.987 -12.27434  0.0000
MonthJul    -44522.34  5373.207  -8.28599  0.0000
MonthAug    -29768.74  5365.559  -5.54812  0.0000
MonthSep    -12039.27  5331.948  -2.25795  0.0252
MonthOct     26393.95  5238.620   5.03834  0.0000
MonthNov     16471.67  4988.022   3.30224  0.0012
MonthDec    -58631.94  4272.401 -13.72342  0.0000

 Correlation: 
         (Intr) Time   MnthFb MnthMr MnthAp MnthMy MnthJn MnthJl MnthAg MnthSp
Time     -0.586                                                               
MonthFeb -0.447  0.003                                                        
MonthMar -0.525 -0.001  0.589                                                 
MonthApr -0.551 -0.005  0.462  0.659                                          
MonthMay -0.558 -0.011  0.416  0.535  0.682                                   
MonthJun -0.559 -0.016  0.398  0.487  0.560  0.690                            
MonthJul -0.557 -0.022  0.391  0.468  0.512  0.568  0.692                     
MonthAug -0.552 -0.028  0.387  0.460  0.492  0.520  0.571  0.692              
MonthSep -0.545 -0.034  0.383  0.454  0.481  0.498  0.520  0.569  0.690       
MonthOct -0.532 -0.039  0.376  0.445  0.470  0.482  0.493  0.513  0.561  0.683
MonthNov -0.502 -0.044  0.358  0.423  0.446  0.456  0.463  0.471  0.491  0.538
MonthDec -0.426 -0.048  0.308  0.364  0.384  0.392  0.396  0.400  0.407  0.425
         MnthOc MnthNv
Time                  
MonthFeb              
MonthMar              
MonthApr              
MonthMay              
MonthJun              
MonthJul              
MonthAug              
MonthSep              
MonthOct              
MonthNov  0.662       
MonthDec  0.471  0.597

Standardized residuals:
       Min         Q1        Med         Q3        Max 
-2.5656600 -0.6285951 -0.1307054  0.5424996  3.2823396 

Residual standard error: 14799.38 
Degrees of freedom: 180 total; 167 residual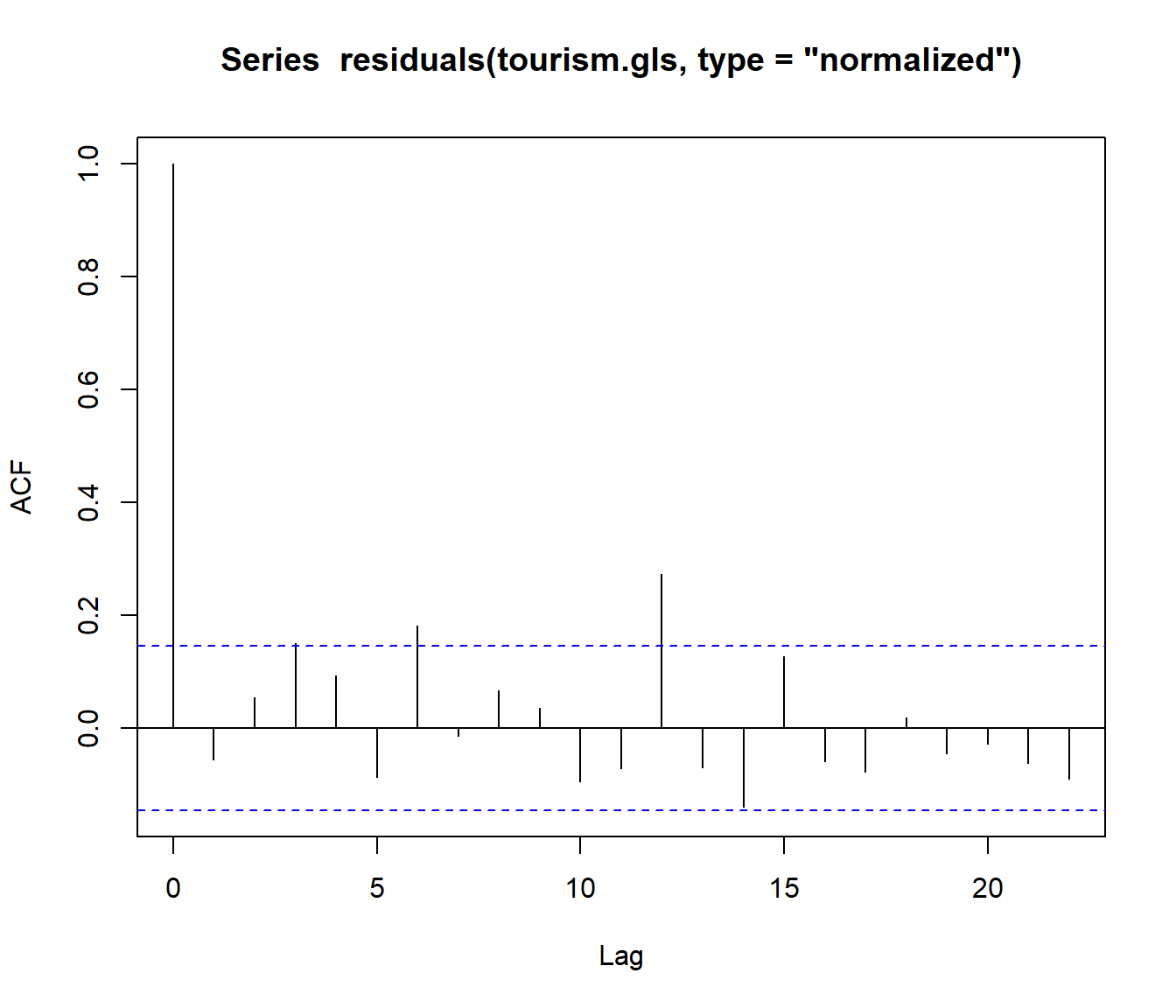

32.15 Comments on the Analysis

The estimated value of AR1 correlation parameter is \(\hat \phi = 0.393\).

Comparison of the output from summary(tourism.gls) with the corresponding output from the earlier analysis (assuming independent errors) shows that the standard errors are usually larger here, particularly for the intercept and the coefficient of Time:

# A tibble: 2 × 4
  model term  estimate std.error
  <chr> <chr>    <dbl>     <dbl>
1 gls   Time     1062.      31.9
2 lm    Time     1059.      21.2

The only remaining question is, was the use of gls() successful?

We can get the normalized residuals (i.e. ‘decorrelated’ residuals) with

residuals(tourism.gls, type = "normalized")

32.16 

acf(residuals(tourism.gls, type = "normalized"))

unlabelled

32.17 Next steps?

What might be the next step? It looks like there is a significant 12-month correlation, which would also make sense.

But we will leave the task of adjusting for more complicated correlation structures for another course.